فرم معتبر نیست.
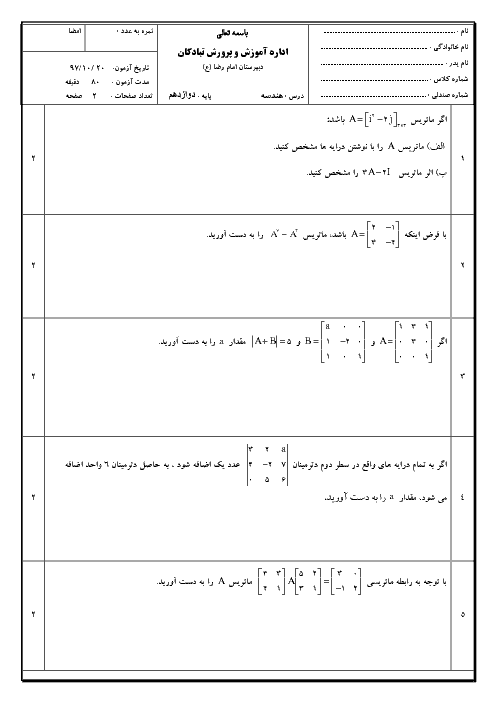
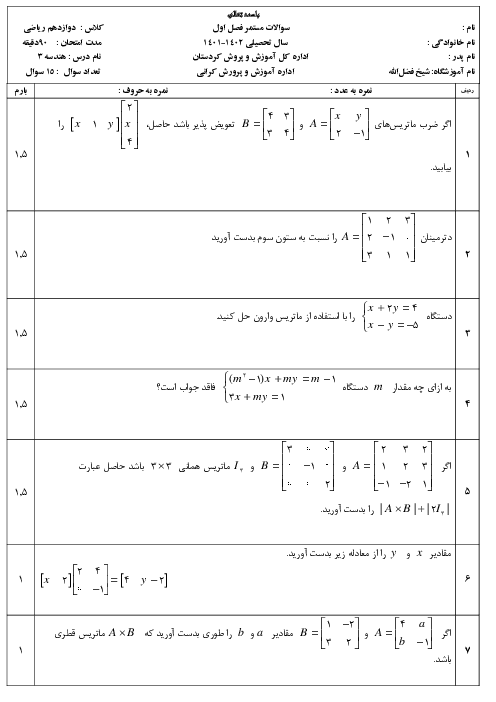
اندازهٔ وتری که دایره $C:{x^2} + {y^2} - 8x = 34$ روی خط $3x - 4y + 13 = 0$ جدا میکند را به دست آورید.
پاسخ تشریحی :
نمایش پاسخ
$C:{x^2} + {y^2} - 8x = 34 \to O = (4,0),r = \sqrt {50} $
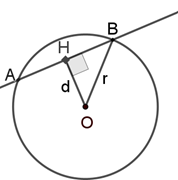
فاصله مرکز دایره تا خط برابر است با:
$OH = \frac{{\left| {3(4) - 4(0) + 13} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{25}}{5} = 5$
قطر عمود بر وتر آن را نصف میکند، بنا بر رابطه فیثاغورس در مثلث داریم:
$B{H^2} + O{H^2} = {r^2} \to B{H^2} + 25 = 50 \to BH = 5,AB = 2BH = 10$
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...