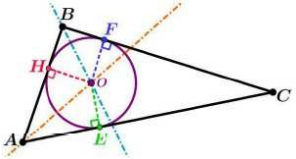
مثلثی دلخواه رسم کنید و آن را $ABC$ بنامید. نیمسازهای دو زاویهٔ این مثلث را رسم کنید و نقطهٔ برخورد آنها را $O$ بنامید. از نقطهٔ $O$ بر سه ضلع مثلث عمود رسم کنید و پای یکی از عمودها را $H$ بنامید. به مرکز $O$ و به شعاع $OH$ دایره‌ای رسم کنید. اضلاع مثلث $ABC$ نسبت به این دایره چه وضعیتی دارند؟ چرا؟
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...