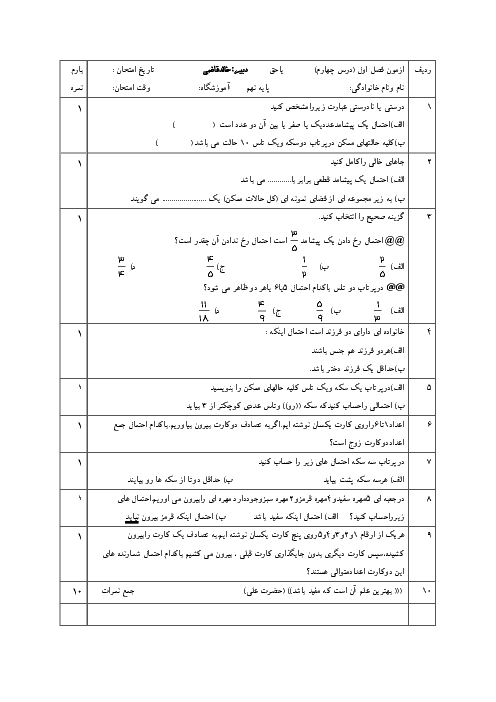
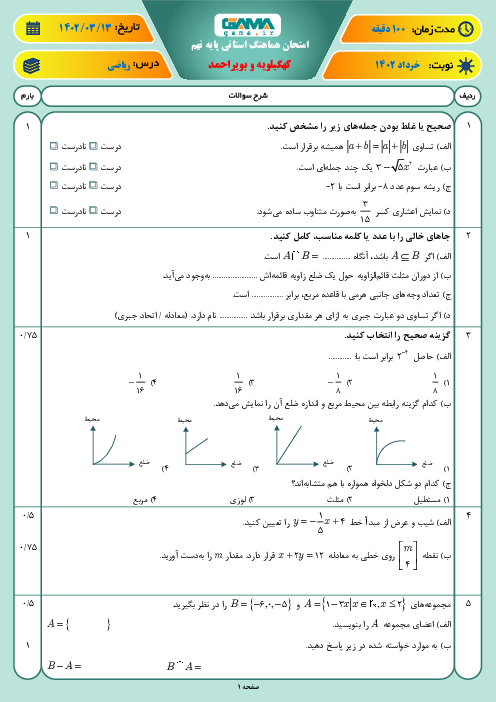
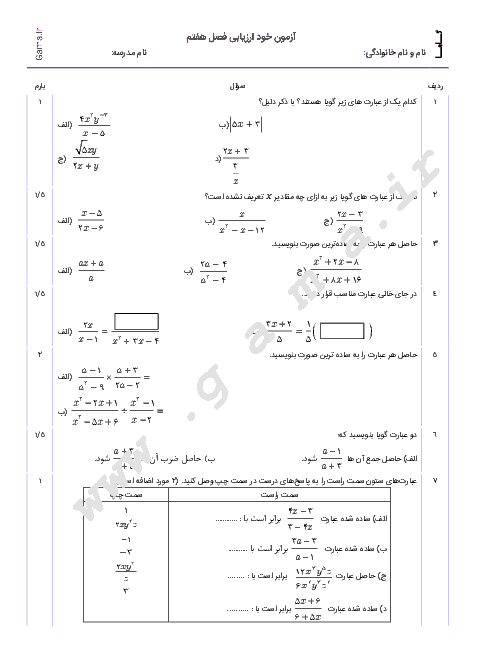
گزینه 1: در واقع خطوط موازی در دستگاه معادلات بدون پاسخ خواهند بود و چون این خطوط شیب برابری دارند و فقط عرض از به مبدأ متفاوت است پس از حل دستگاه با روش حذفی به پاسخ $O = k$ می‌رسیم. پس این گزینه درست است.

گزینه 2: خط با شیب مثبت و عرض از مبدأ منفی از ناحیهٔ 2 فقط عبور نمی‌کند. بنابراین این گزینه نادرست است.

گزینه 3: در معادلهٔ خط مقادیر y برحسب x در معادلهٔ خط به دست می‌آیند پس جمله درست است.

گزینه 4: یک عبارت جبری زمانی اتحاد است که عبارت در دو سمت تساوی هم درجه بوده و ضرایب هم درجه‌ها برابر باشند.

${(x + y)^2} = {x^2} + {y^2} + 2xy \ne {x^2} + {y^2}$

از طرفی عبارات اتحاد جبری به ازای هر عددی صحیح هستند.

مثلا $x = 2\,,\,y = 4 \to \begin{array}{*{20}{c}}
  {{{(x + y)}^2} = {{(5)}^2} = 25} \\ 
  {{x^2} + {y^2} = 4 + 9 = 13} 
\end{array} \to 25 \ne 13$