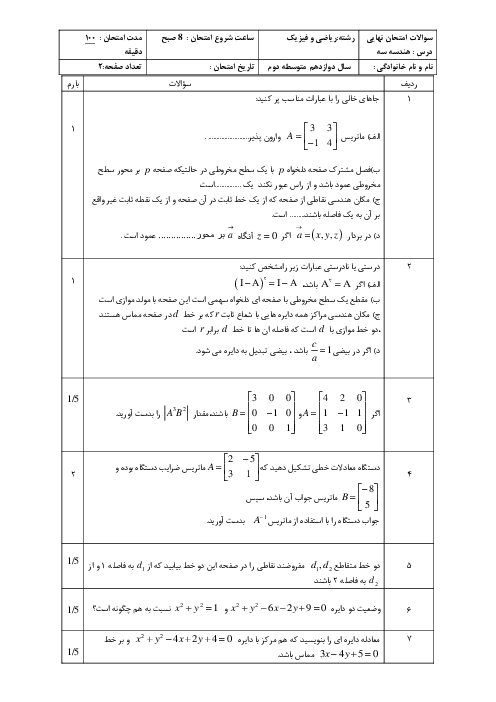
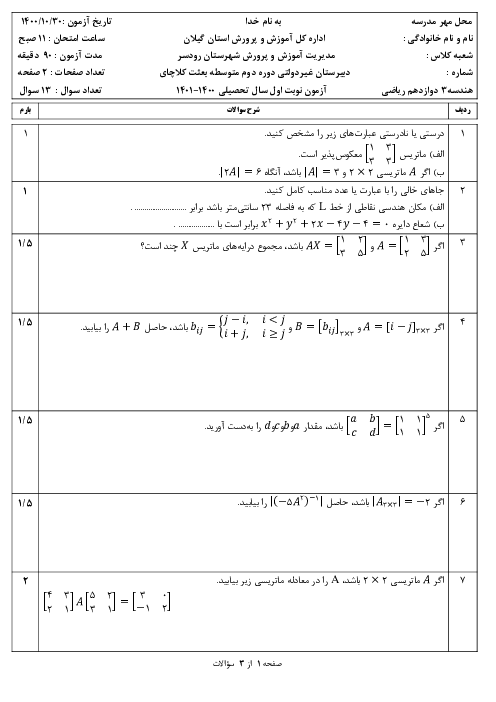
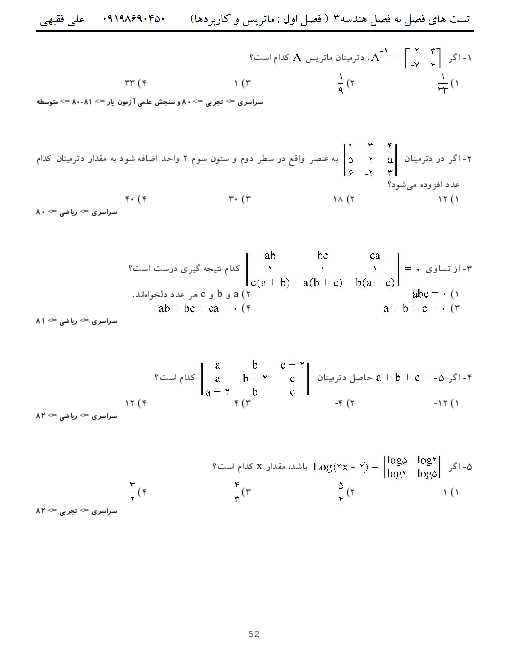
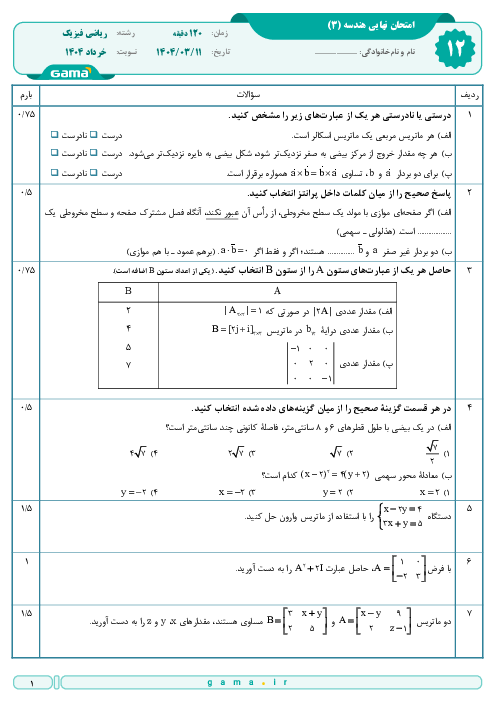
درس 1: آشنایی با مقاطع مخروطی و مکان هندسی
هندسه (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
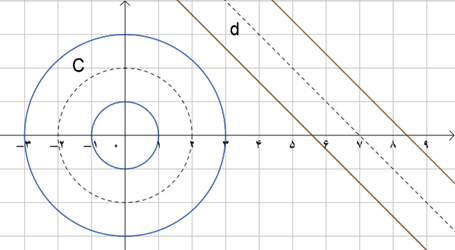
دایره به معادله $C:{x^2} + {y^2} = 4$ و خط $d:x + y = 7$ مفروض‌اند. مکان هندسی مرکز دایره‌های به شعاع واحد را بیابید که هم بر دایره C و هم بر خط d مماس باشد. مسأله چند جواب دارد؟
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...