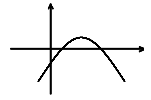
اگر نمودار تابع $f\left( x \right) = m{x^2} + 8x - 2$ به صورت زیر باشد، m چند مقدار صحیح میتواند داشته باشد.

گاما رو نصب کن!
جستجو
پربازدیدها: #{{ tag.title }}
به پاس اعتمادی که به گاما داشتی، ما اشتراک ویژهای رو برات فعال کردیم تا بدون هیچ نگرانی از محدودیت زمانی، از سرویسهای ویژه گاما استفاده کنی.
اگه به اطلاعات بیشتری نیاز داری راهنمای تغییرات جدید رو ببین.
از همراهیت با گاما سپاسگزاریم.
با تقدیم احترام
با سپاس! گزارش شما ثبت شد.