$\left| OA \right|=\sqrt{{{(m+1)}^{2}}+1+4}=\sqrt{{{(m+1)}^{2}}+5}$
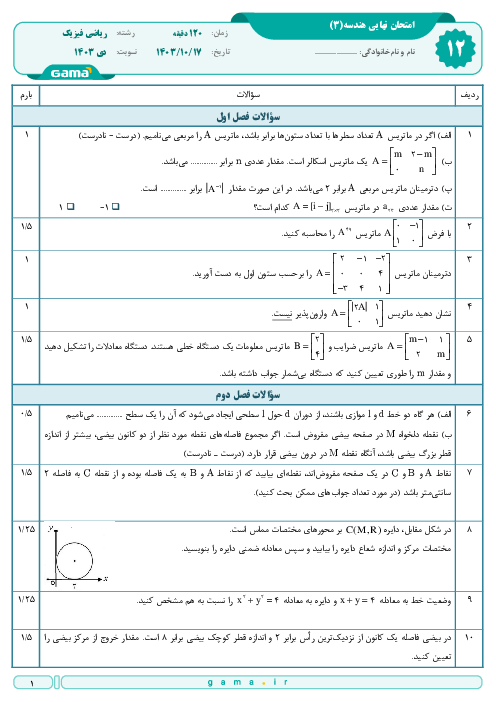
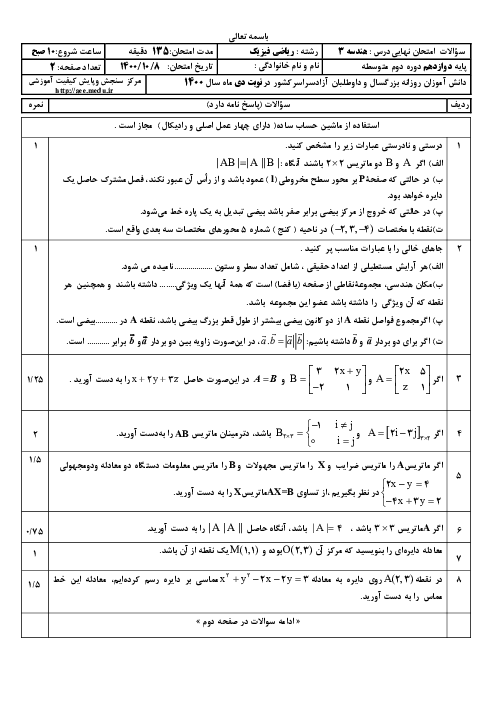
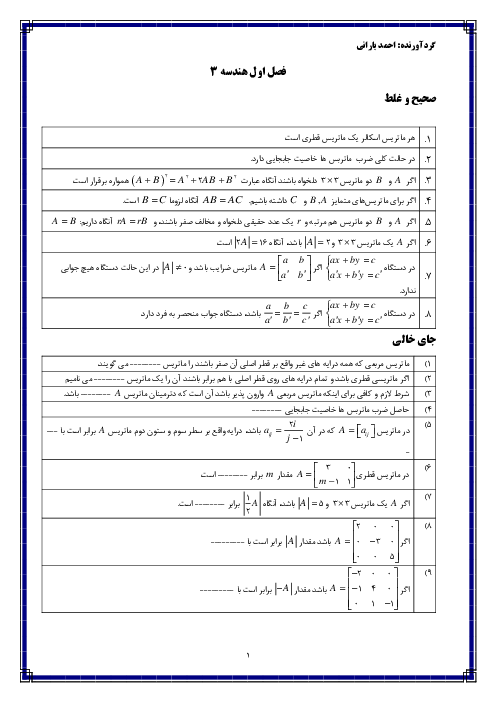
$\left| OB \right|=\sqrt{{{m}^{2}}+1+1}=\sqrt{{{m}^{2}}+2}$
$\left| AB \right|=\sqrt{{{(m-m-1)}^{2}}+{{(-1-1)}^{2}}+{{(1+2)}^{2}}}=\sqrt{14}$
${{\left| AB \right|}^{2}}\gt {{\left| OA \right|}^{2}}\Rightarrow 14\gt {{(m+1)}^{2}}+5\Rightarrow {{(m+1)}^{2}}\lt 9$
$\Rightarrow -4\lt m\lt 2$
${{\left| OA \right|}^{2}}\gt {{\left| OB \right|}^{2}}\Rightarrow {{(m+1)}^{2}}+5\gt {{m}^{2}}+2\Rightarrow m\gt -2$
از اشتراک نامعادلات فوق، حدود تغییرات $m$ بهصورت $-2\lt m\lt 2$ بهدست میآید.