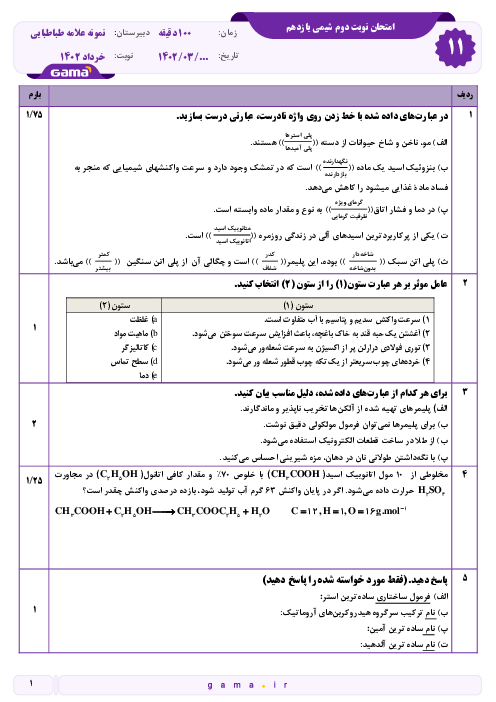
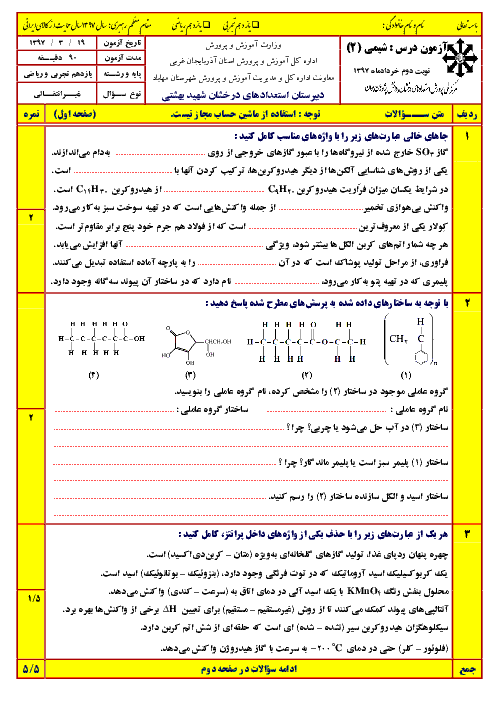
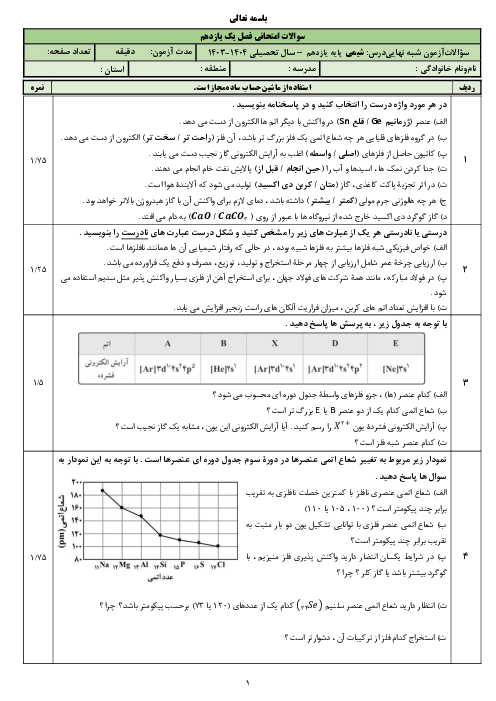
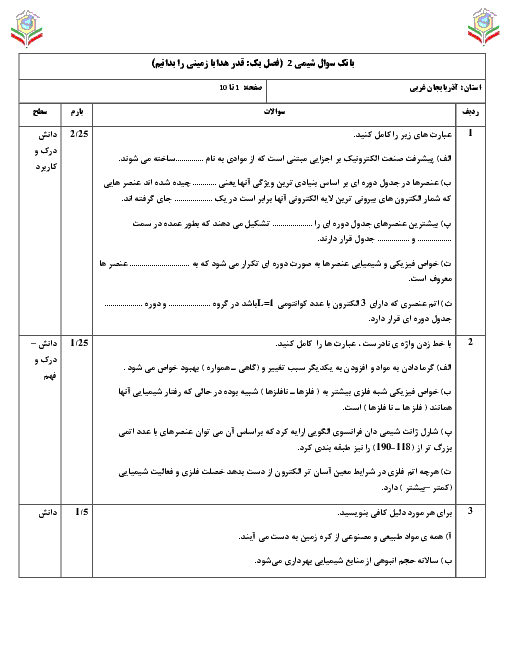
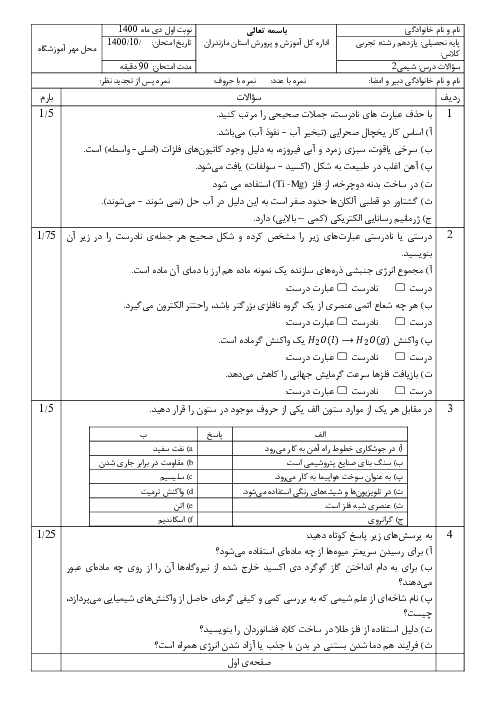
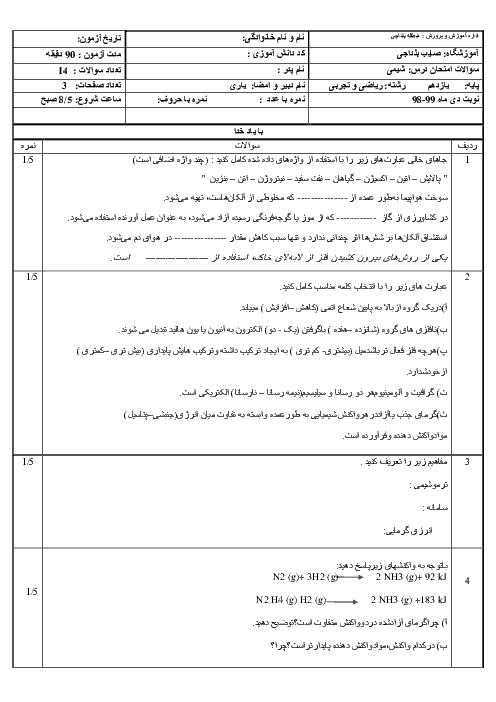
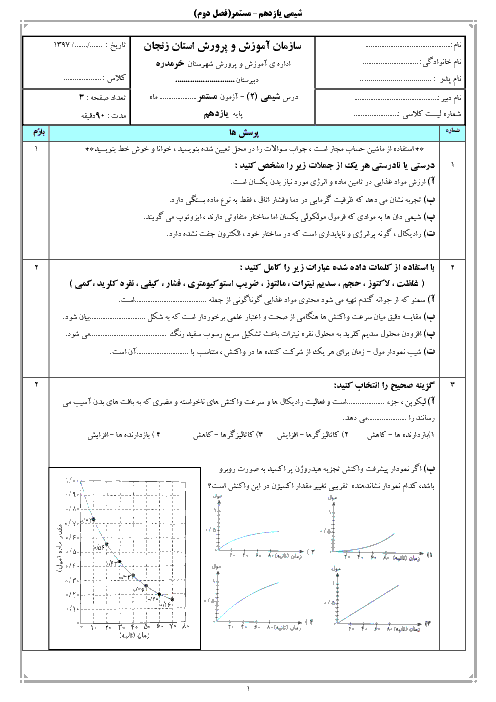
اگر در واکنش یک تیغۀ 20 گرمی فلز روی با 100 میلیلیتر محلول نیممولار مس (II) سولفات تغییر جرم تیغه در مدت زمان 3 دقیقه برابر 0/6 گرم باشد، سرعت مصرف محلول مس (II) سولفات چند $\frac{\mathrm{mol}}{L \cdot \mathrm{~min}}$است؟
$\left(Z n=65, C u=64: g \cdot \mathrm{~mol}^{-1}\right)$ (با فرض اینکه تمام اتمهای مس بر روی تیغه فلز روی قرار گرفته باشند.) $\mathrm{Zn}(s)+\mathrm{CuSO}_4(a q) \rightarrow \mathrm{ZnSO}_4(a q)+\mathrm{Cu}(s)$
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...