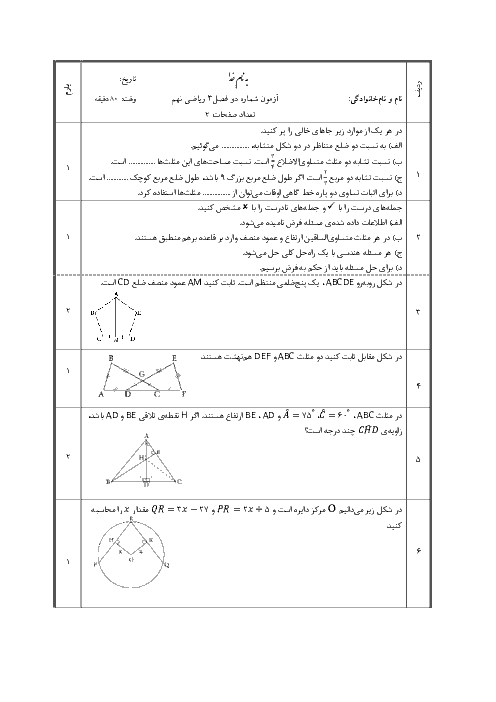
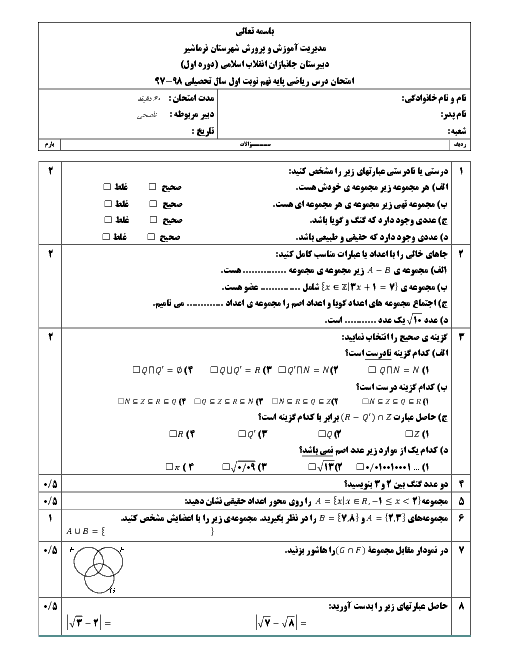
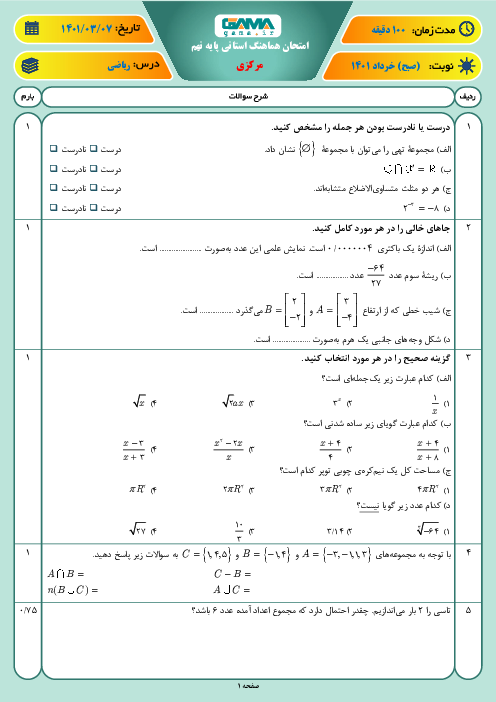
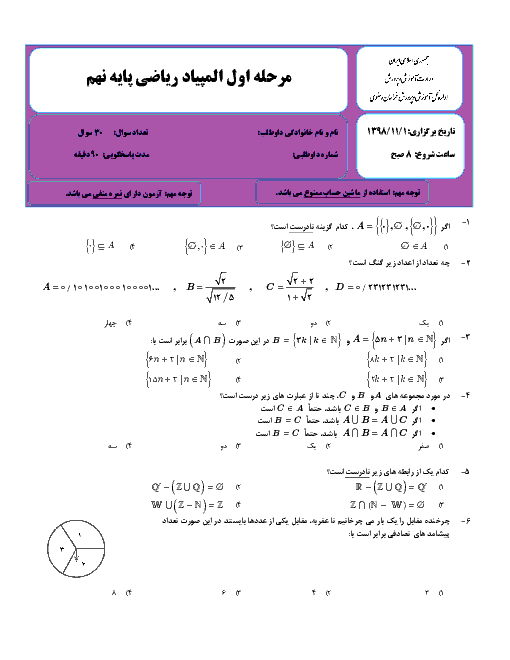
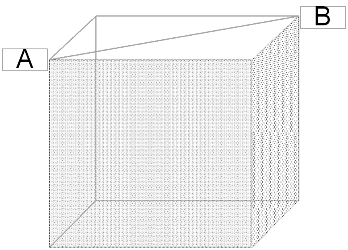
یک اسفنج مکعب شکل به ضلع 3b را در راستای پاره خط AB بریده‌ایم، مساحت کل یکی از قسمت‌های ایجاد شده چقدر است؟
1 )
$ 3\sqrt{2}b^2 $
2 )
$ (18\sqrt{2} + 54)b^2 $
3 )
$27b^2 $
$ (27 + 9\sqrt{2})b^2 $
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...