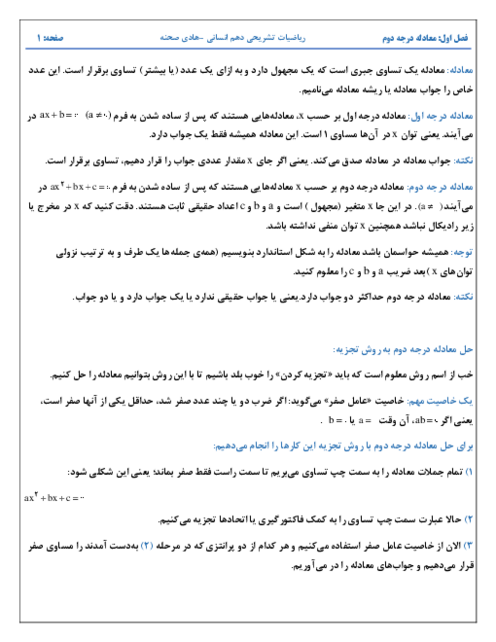
درس 2: حل معادلۀ درجۀ 2 و کاربردها
ریاضی و آمار (1)
دهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
معادلهٔ درجهٔ دوم $2{x^2} + ax - 5 = 0$ را با استفاده از روش مربع کامل به صورت ${(x - \frac{3}{4})^2} = b$ نوشتهایم، $a + b$ کدام است؟
1 )
$\frac{{97}}{{16}}$
$\frac{1}{{16}}$
3 )
$ - \frac{7}{{16}}$
4 )
$\frac{{79}}{{16}}$