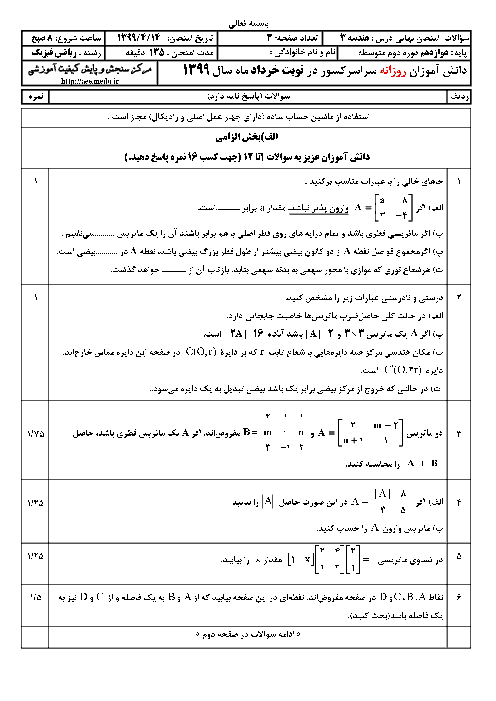
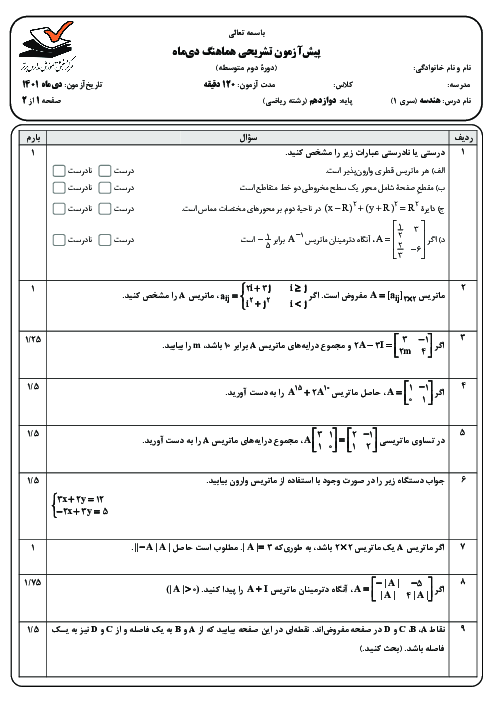
بیضی با قطر بزرگ 2a، قطر کوچک 2b و کانونهای $F$ و $F'$ مطابق شکل روبهرو مفروض است. اگر خطی در کانون F بر قطر کانونی عمود باشد و بیضی را در نقطه D قطع کند، ثابت کنید: $DF = \frac{{{b^2}}}{a}$
پاسخ تشریحی :

تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!