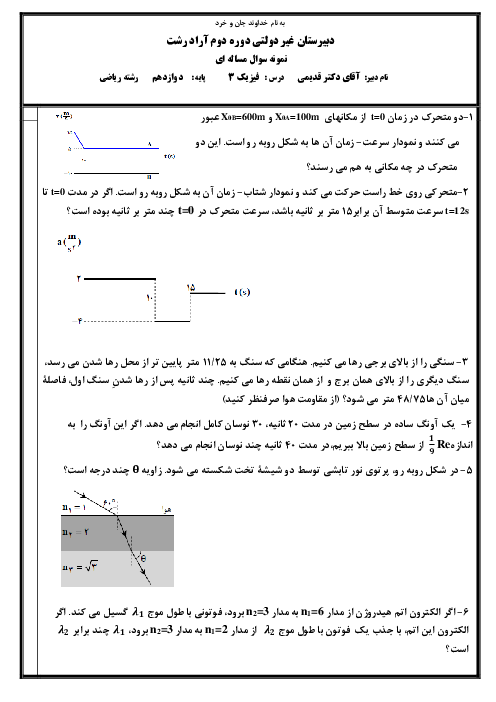
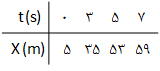متحركی كه روی خط راست حركت می‌كند، در بازه‌ی زمانی تا ، با سرعت ثابت و از لحظه‌ی تا ، با شتاب ثابت و از به بعد با سرعت ثابت حركت می‌كند. جدول زير، مكان متحرک را… | فیزیک (3) ریاضی دوازدهم شماره 79808

موبایل / ایمیل

لطفا کدی که به {{ identity }} ارسال شده است را وارد کنید.

کد فعال سازی :

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

لطفا برای حساب خود رمز عبور انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل / ایمیل

لطفا کدی که برای شما ارسال شده است را وارد کنید.

کد فعال سازی :

ارسال مجدد کد فعال سازی {{ countDown }}

منتظر دریافت پیامک شما ...

برای حساب خود رمز عبور جدید انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

ورود | ثبت نام

لطفا کمی صبر کنید ...

موبایل / ایمیل

رمزعبور

رمز عبور خود را فراموش کردید؟ بازیابی کنید.

هنوز عضو نشده اید؟ ثبت نام کنید.

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

** فصل 1: حرکت بر خط راست فیزیک (3) ریاضی دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

متحركی كه روی خط راست حركت می‌كند، در بازه‌ی زمانی $t=0$ تا $t=4s$، با سرعت ثابت و از لحظه‌ی $t=4s$ تا $t=6s$، با شتاب ثابت و از $t=6s$ به بعد با سرعت ثابت حركت می‌كند. جدول زير، مكان متحرک را در برخی زمان‌های حركت، نشان می‌دهد. متحرک در $t=10s$ از چه مكانی می‌گذرد؟

1 )

$x=65m$

2 )

$x=63m$

3 )

$x=69m$

4 )

$x=67m$

نمایش پاسخ

در قسمت اول حركت (بازه‌ی $t=0$ تا $t=4s$) حركت متحرک سرعت ثابت است و داريم:

$_{x=vt+{{x}_{{}^\circ }}\Rightarrow x(4s)=10\times 4+5=45m}^{v={{v}_{av}}=\frac{\Delta x}{\Delta t}=\frac{35-5}{3-0}=10\frac{m}{s}}$

در قسمت دوم حركت (يعنی از $t=4s$ تا $t=6s$)، شتاب ثابت است و سرعت اوليه‌ی اين قسمت، همان $v(4s)$ یعنی $10\frac{m}{s}$ است. برای بازه‌ی زمانی $t=4s$ تا $t=5s$، داریم:

$_{v=at+{{v}_{{}^\circ }}\Rightarrow v(6s)=-4\times 2+10=2\frac{m}{s}}^{\Delta x=\frac{1}{2}a{{t}^{2}}+{{v}_{{}^\circ }}t\Rightarrow 53-45=\frac{1}{2}a\times {{1}^{2}}+10\times 1\Rightarrow 8=\frac{a}{2}+10\Rightarrow a=-4\frac{m}{{{s}^{2}}}}$

در قسمت سوم حركت (از لحظه‌ی $t=6s$ به بعد) حركت متحرک سرعت ثابت است و سرعت متحرک همان $v(6s)$ یعنی $2\frac{m}{s}$ است، بنابراین:

$\Delta x=v\Delta t\Rightarrow x(10s)-59=2\times 3\Rightarrow x(10s)=65m$

گزارش خطا