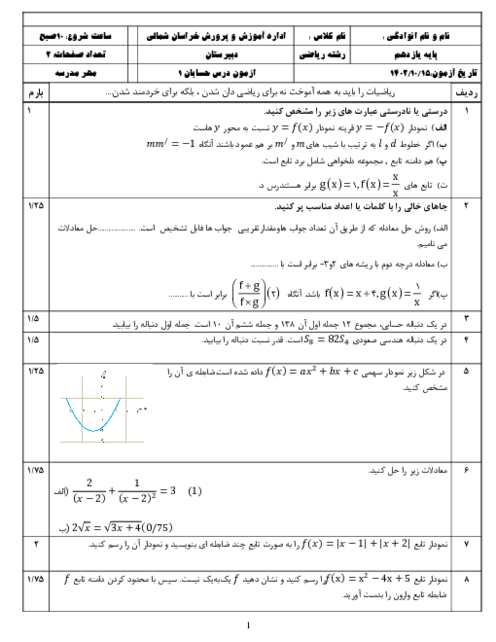
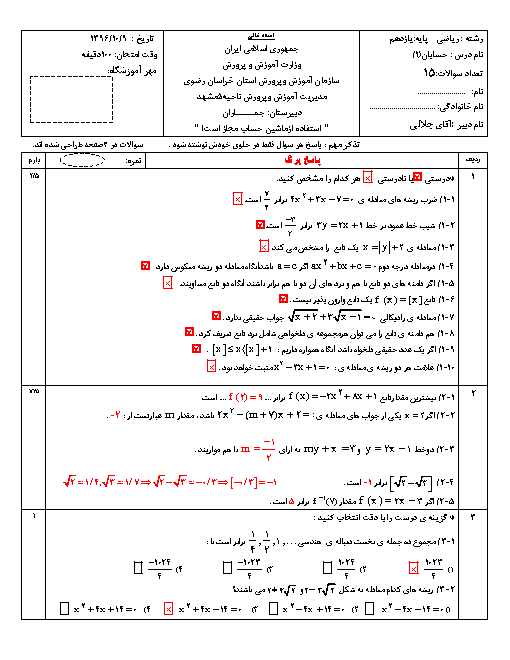
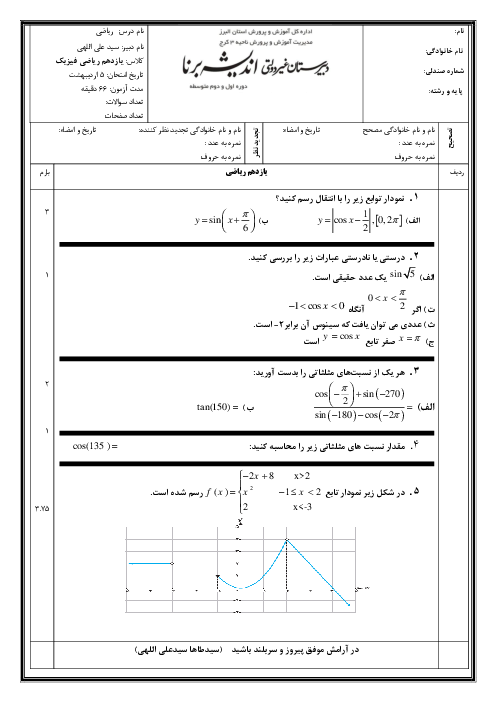
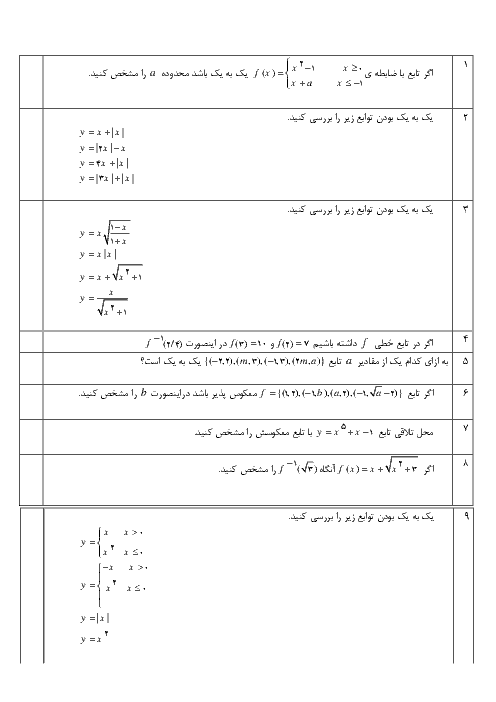
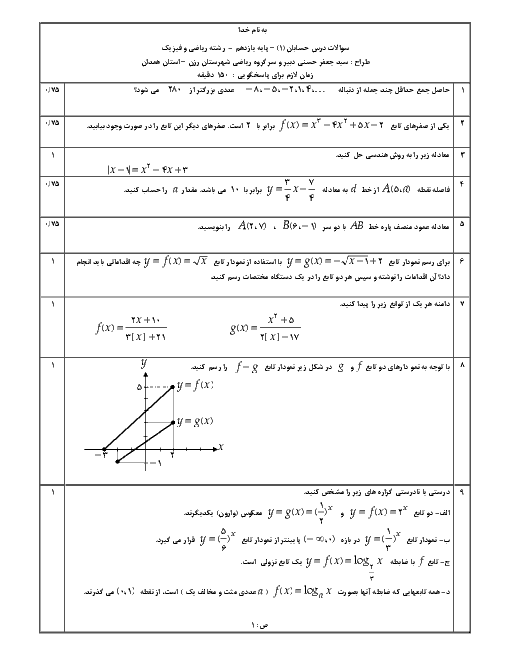
تابع f با ضابطهٔ $f(x) = \left\{ {\begin{array}{*{20}{c}} {\frac{{2a(\sqrt {x + 3} - 2)}}{{\left| {x - 1} \right|}}}&{x < 1} \\ {\left[ {x - 1} \right] + 1}&{x \geqslant 1} \end{array}} \right.$ مفروض است. a را چنان بیابید که تابع در $x = 1$ حد داشته باشد.
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...