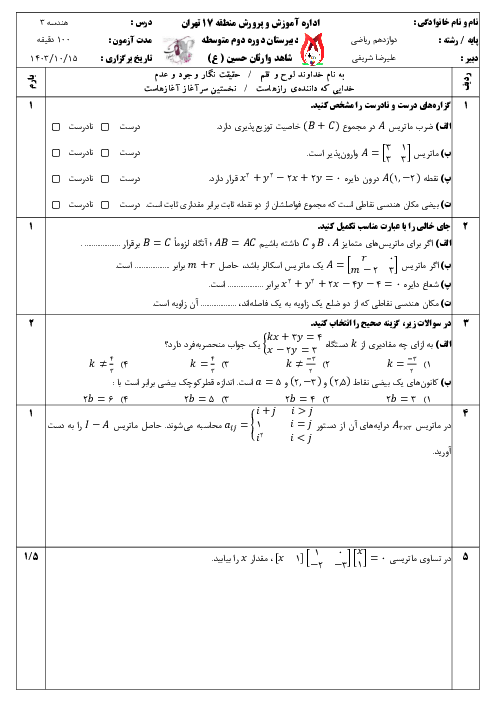
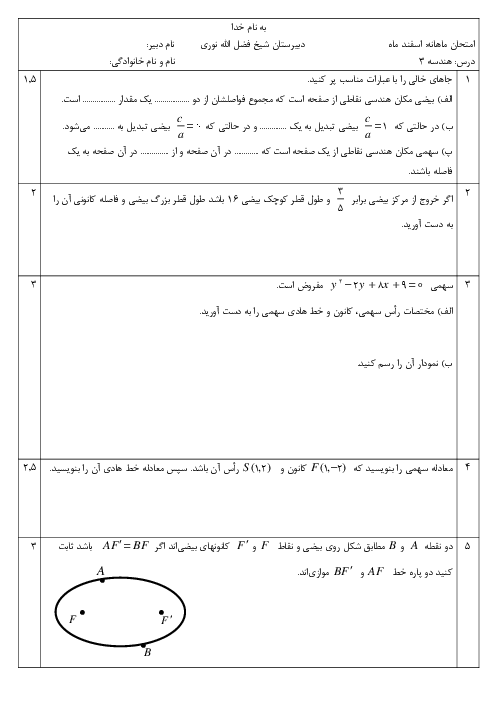
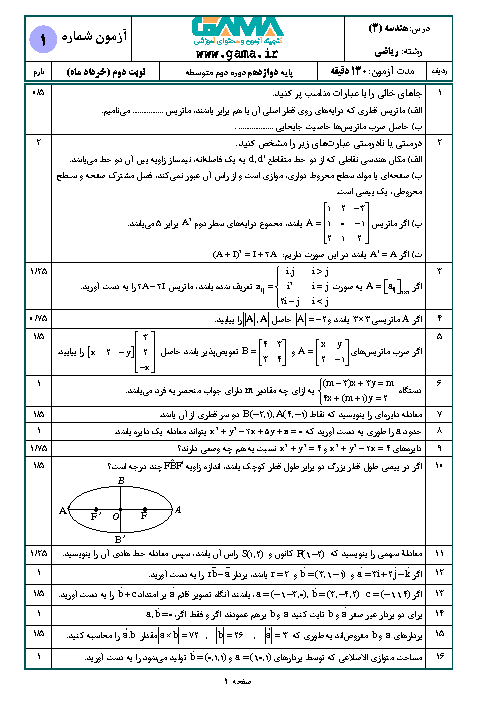
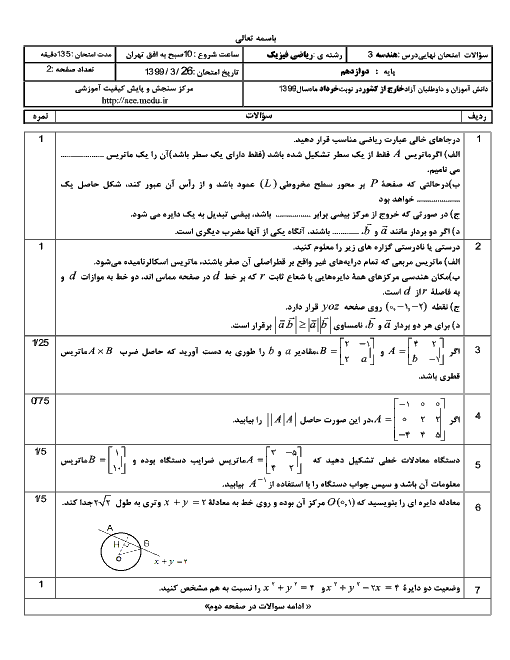
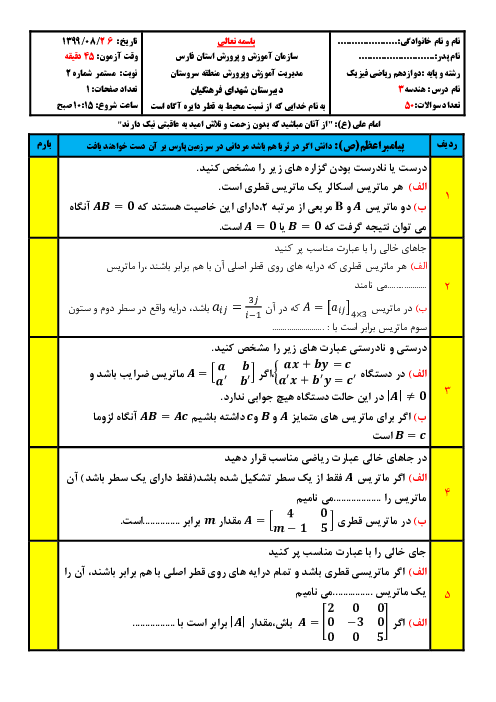
طول قطرهای بزرگ و کوچک یک بیضی به ترتیب 2a و 2b است. قطر یک دایره منطبق بر قطر بزرگ بیضی است. از کانون F بیضی، عمودی بر محور کانونی رسم میکنیم تا دایره را در نقطهای مانند M قطع کند. ثابت کنید MF با نصف قطر کوچک بیضی برابر است.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!