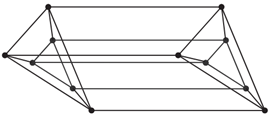
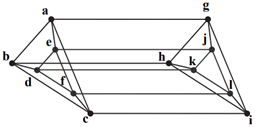
يک ايستگاه ماهواره‌ای در اطراف كرهٔ زمين با ۱۲ فرستنده را در نظر بگيريد كه در آن هر فرستنده مطابق شكل زير، با چند ماهوارهٔ ديگر ارتباط ماهواره‌ای دوطرفه دارد. گراف…

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

درس 2: مدل‌سازی با گراف ریاضیات گسسته دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

يک ايستگاه ماهواره‌ای در اطراف كرهٔ زمين با ۱۲ فرستنده را در نظر بگيريد كه در آن هر فرستنده مطابق شكل زير، با چند ماهوارهٔ ديگر ارتباط ماهواره‌ای دوطرفه دارد. گراف زير يک مدل‌سازی از شبكۀ ماهواره‌ای موردنظر است كه در آن هر رأس يک فرستنده و يال بين دو رأس نمايانگر آن است كه فرستنده‌های نظير به آن دو رأس مستقيماً با هم ارتباط ماهواره‌ای دارند. می‌خواهيم مجموعه‌ای با كم‌ترين تعداد ممكن از فرستنده‌ها (رأس‌ها) انتخاب كنيم به‌طوری كه توسط اين مجموعه از فرستنده‌ها، به تمام فرستنده‌ها وصل باشيم. مجموعۀ انتخاب‌شده حداقل چند عضو دارد؟

1 )

2 )

3 )

4 )

نمایش پاسخ

نكته: در بين تمام مجموعه‌های احاطه‌گر گراف $G$، مجموعه يا مجموعه‌های احاطه‌گری كه كم‌ترين تعداد عضو را دارد، مجموعۀ احاطه‌گر مينيمم و تعداد اعضای چنين مجموعه‌ای را عدد احاطه‌گری گراف $G$ می‌ناميم و با $\gamma (G)$ نمايش می‌دهيم. به مجموعۀ احاطه‌گر مينيمم گراف، يک $-\gamma $ مجموعه هم می‌گوييم.

نکته: در یک گراف $n$ رأسی با ماکزیمم درجهٔ $\Delta $ داریم: $\gamma (G)\ge \left\lceil \frac{n}{\Delta +1} \right\rceil $

$\gamma (G)\ge \left\lceil \frac{12}{5} \right\rceil \Rightarrow \gamma (G)\ge 3$

از طرفی مجموعهٔ $\left\{ d,e,i \right\}$ یک مجموعهٔ احاطه‌گر برای گراف $G$ است؛ پس $\gamma (G)=3$. یعنی با حداقل 3 فرستنده می‌توانیم به تمام فرستنده‌ها وصل باشیم.