قسمت 3: حرکت با شتاب ثابت
فیزیک (3) تجربی
دوازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
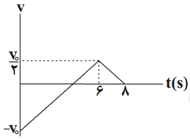
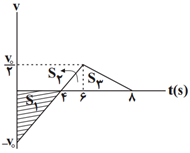
نمودار سرعت - زمان متحرکی که بر روی محور $x$ها حرکت میکند، مطابق شکل مقابل است. مسافت پیموده شده توسط متحرک در مدتی که حرکت آن تندشونده است، چند برابر مسافت پیموده شده توسط متحرک در مدتی است که حرکت آن کندشونده است؟