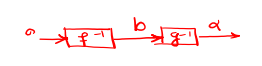
نقطه $(0,\alpha )$ روی این منحنی است $ \leftarrow $ خواسته سوال $y = {g^{ - 1}}o{f^{ - 1}}(x)$ است.

${f^{ - 1}}(0) \to f(b) = 0 \to \log (2b - 5) = 0 \to 2 - 5 = 1 \to b = 3$

${g^{ - 1}}(3) = \alpha  \to g(\alpha ) = 3 \to \alpha  + \sqrt {2\alpha  - 4}  = 3 \to \sqrt {2\alpha  - 4}  = 3 - \alpha  \to $

$\left. \begin{gathered}
  3 - \alpha  \geqslant 0 \hfill \\
  2\alpha  - 4 \geqslant 0 \hfill \\ 
\end{gathered}  \right\}2 \leqslant \alpha  \leqslant 3$

$2\alpha  - 4 = 9 - 6\alpha  + {\alpha ^2} \to {\alpha ^2} - 8\alpha  + 13 = 0 \to \alpha  = 4 \pm \sqrt 3 $

$\alpha  lt 3 \to \alpha  = 4 - \sqrt 3 $