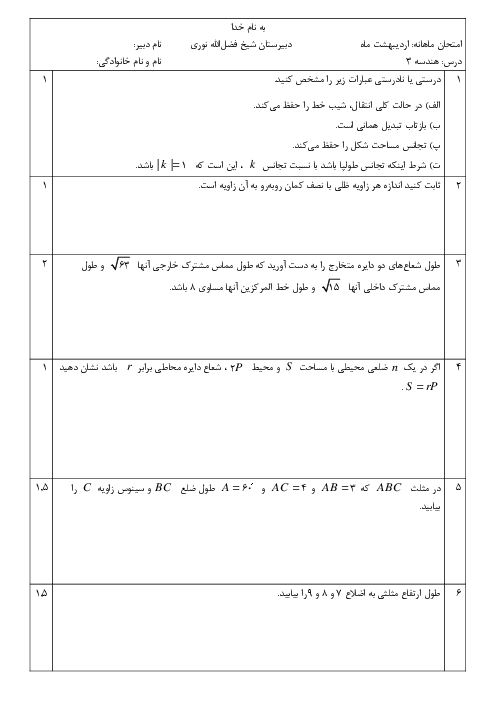
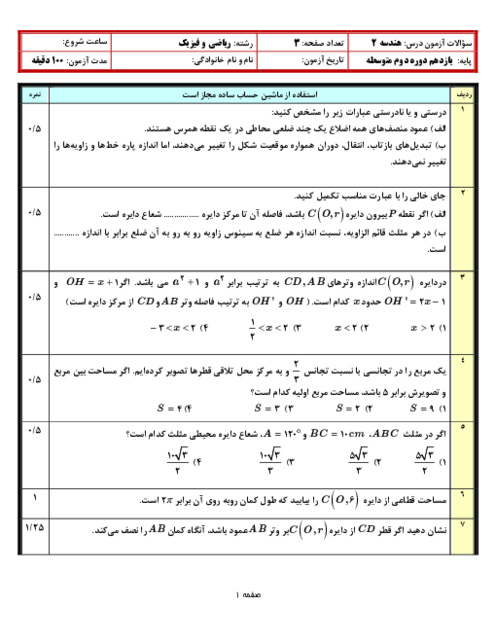
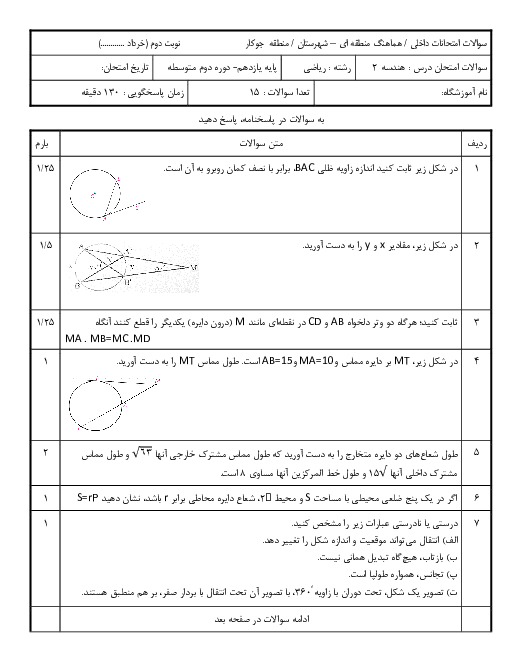
درس 3: چند ضلعی‌های محاطی و محیطی
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
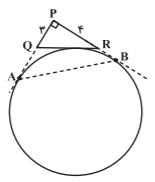
در مثلث قائم‌الزاویه ای به طول ضلع‌های قائمهٔ $3$ و $4$، دایرهٔ محاطی خارجی مماس بر وتر، در نقاط $A$ و $B$ بر امتداد دو ضلع دیگر مماس است. طول $AB$ كدام است؟
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...