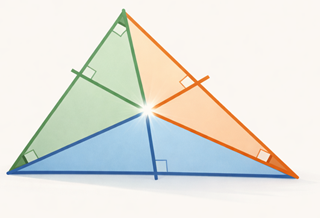
همرسانی ارتفاعها در مثلث: یک ملاقات در نقطهای جادویی به نام مرکز ارتفاعی
ارتفاع چیست؟ از تعریف پایه تا رسم عمود
برای درک این همرسانی جالب، ابتدا باید بدانیم ارتفاع در یک مثلث چیست. ارتفاع هر ضلع، پارهخطی است از رأس مقابل آن ضلع، که بر آن ضلع عمود است. به زبان سادهتر، اگر خطکش را به گونهای روی رأس مثلث بگذاریم که با ضلع مقابلش زاویهٔ $90^\circ$ (قائمه) بسازد، خط رسمشده همان ارتفاع است.
برای مثال، در مثلث $\triangle ABC$:
• ارتفاع مربوط به ضلع $BC$ از رأس $A$ رسم میشود.
• ارتفاع مربوط به ضلع $AC$ از رأس $B$ رسم میشود.
• ارتفاع مربوط به ضلع $AB$ از رأس $C$ رسم میشود.
چرا ارتفاعها در یک نقطه مشترک میشوند؟ (ایدهای برای اثبات)
این یک حکم کلی در هندسه است و میتوان آن را با چندین روش اثبات کرد. یکی از روشهای قابلدرک برای سطح متوسطه، استفاده از مفهوم مثلث القایی۵ یا مثلث متعامدپا۶ است.
گامبهگام:
1. مثلث اصلی را $\triangle ABC$ در نظر بگیرید.
2. از هر رأس، خطی موازی با ضلع مقابل آن رسم کنید. این سه خط، یک مثلث جدید و بزرگتر به نام $\triangle A'B'C'$ میسازند.
3. با استفاده از ویژگیهای متوازیالاضلاع و خطوط موازی، میتوان نشان داد که نقاط $A,B,C$ وسط اضلاع مثلث جدید هستند.
4. در این حالت، ارتفاعهای مثلث اصلی ($\triangle ABC$) دقیقاً همان عمودمنصفهای۷ مثلث جدید ($\triangle A'B'C'$) خواهند بود.
5. میدانیم که سه عمودمنصف هر مثلث در یک نقطه (مرکز دایرهٔ محیطی۸) همدیگر را قطع میکنند.
6. بنابراین، سه ارتفاع مثلث اصلی نیز در یک نقطه مشترک خواهند بود. این نقطه، مرکز ارتفاعی مثلث اصلی است.
مرکز ارتفاعی کجا قرار میگیرد؟ نقشهکشی برای انواع مثلث
موقعیت مرکز ارتفاعی نسبت به مثلث، ثابت نیست و به شکل مثلث بستگی دارد. این تنوع، موضوع را جذابتر میکند.
| نوع مثلث | توضیح | موقعیت مرکز ارتفاعی (H) |
|---|---|---|
| تندگوشه۹ | همهٔ زوایای داخلی کوچکتر از 90° هستند. | داخل مثلث قرار میگیرد. |
| راستگوشه۱۰ | یک زاویه دقیقاً برابر 90° است. | بر رأس زاویهٔ قائمه منطبق میشود. (مثال ساده: در مثلث قائمالزاویه با زاویهٔ قائمه در A، مرکز ارتفاعی نقطهٔ A است) |
| بازگوشه۱۱ | یک زاویه بزرگتر از 90° است. | خارج مثلث قرار میگیرد. |
برای درک بهتر، یک مثلث بازگوشه روی کاغذ بکشید. هنگام رسم ارتفاع از رأس زاویهٔ باز، میبینید که این ارتفاع به ادامهٔ ضلع مقابل (نه خود ضلع) عمود میشود و نقطهٔ تقاطع سه ارتفاع در خارج از محدودهٔ مثلث اصلی شکل میگیرد.
ارتفاعها در عمل: از طراحی ساختمان تا یافتن بزرگترین مساحت
شاید بپرسید این مفهوم به چه دردی میخورد؟ کاربردهای عملی آن را در اطراف خود میبینیم.
مثال ۱: پایداری سازه. در مهندسی عمران، برای طراحی سقفهای شیروانی یا سازههای مثلثی، یافتن نقطهٔ تقاطع اجزای حمایتکننده (که شبیه به ارتفاع عمل میکنند) میتواند به توزیع متعادل وزن و پایداری بیشتر کمک کند.
مثال ۲: محاسبهٔ مساحت. فرمول کلاسیک مساحت مثلث: $ \frac{1}{2} \times \text{قاعده} \times \text{ارتفاع}$. برای محاسبهٔ مساحت، باید ارتفاع مربوط به یک قاعده را بدانیم. اگر ارتفاعها را رسم کنیم و طول آنها را اندازه بگیریم، میتوانیم مساحت را از سه راه مختلف (با سه قاعدهٔ مختلف) حساب کنیم که باید جواب یکسانی بدهد. این یک روش عالی برای صحتسنجی محاسبات است.
مثال ۳: بازی و معمّا. در برخی بازیهای فکری یا مسائل بهینهسازی، گاهی نیاز است کوتاهترین فاصله از یک نقطه (رأس) به یک خط (ضلع) را پیدا کنیم. این دقیقاً همان تعریف ارتفاع است. اگر سه شرط مشابه داشته باشیم، نقطهای که این سه شرط را بهطور همزمان بهینه کند، میتواند مرکز ارتفاعی باشد.
پرسشهای مهم و اشتباهات رایج دانشآموزان
پاورقی
۱. ارتفاع (Altitude): پارهخطی عمود بر یک ضلع مثلث که از رأس مقابل آن ضلع میگذرد.
۲. مرکز ارتفاعی (Orthocenter): نقطهٔ تقاطع سه ارتفاع یک مثلث.
۳. ارتو سنتر (Orthocenter): معادل انگلیسی مرکز ارتفاعی.
۴. همرسانی (Concurrency): وضعیتی که در آن سه یا چند خط در یک نقطه مشترک باشند.
۵. مثلث القایی (Anticomplementary Triangle): مثلثی که با رسم خطوط موازی با اضلاع مثلث اصلی از رئوس مقابل به وجود میآید.
۶. مثلث متعامدپا (Pedal Triangle): مثلثی که رئوس آن، پایهای عمودهای (ارتفاعهای) یک نقطه بر اضلاع مثلث اصلی هستند. (در اینجا نقطه، مرکز ارتفاعی است)
۷. عمودمنصف (Perpendicular Bisector): خطی که یک پارهخط را در نقطهٔ وسط آن قطع کرده و بر آن عمود است.
۸. مرکز دایرهٔ محیطی (Circumcenter): مرکز دایرهای که از سه رأس مثلث میگذرد. نقطهٔ تقاطع عمودمنصفها.
۹. تندگوشه (Acute Triangle): مثلثی که هر سه زاویهٔ آن کمتر از ۹۰ درجه باشد.
۱۰. راستگوشه (Right Triangle): مثلثی که یک زاویهٔ آن دقیقاً ۹۰ درجه باشد.
۱۱. بازگوشه (Obtuse Triangle): مثلثی که یک زاویهٔ آن بیشتر از ۹۰ درجه باشد.
۱۲. میدانهگر (Centroid): نقطهٔ تقاطع سه میدانه (پارهخطی که از یک رأس به وسط ضلع مقابل وصل میشود). همان مرکز ثقل مثلث.
۱۳. خط اویلر (Euler's Line): خطی که از مرکز ارتفاعی، مرکز ثقل و مرکز دایرهٔ محیطی یک مثلث (غیر از متساویالاضلاع) میگذرد.