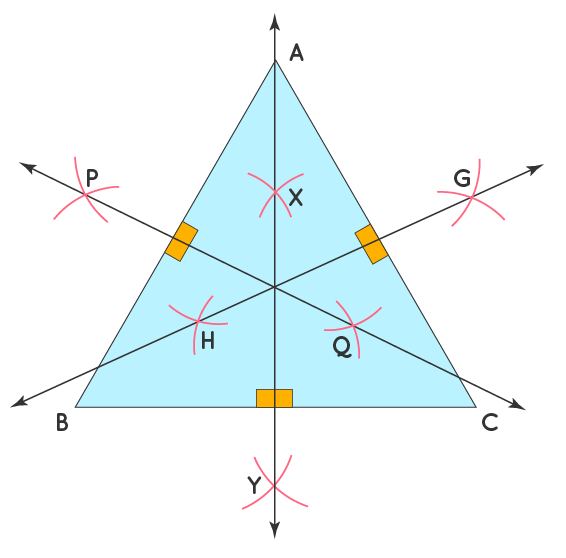
نقطهای که از همهجا یکسان است: همرسانی عمودمنصفها در مثلث
عمودمنصف چیست و چگونه رسم میشود؟
برای درک این قضیه، ابتدا باید با مفهوم عمودمنصف² آشنا شویم. فرض کنید یک پارهخط مانند $ \overline{AB} $ داریم. عمودمنصف این پارهخط، خط راستی است که دو ویژگی مهم دارد:
- از نقطهی وسط پارهخط (نقطهای که فاصلهاش از دو سر $ A $ و $ B $ برابر است) میگذرد.
- بر خود پارهخط $ \overline{AB} $عمود است (یعنی با آن زاویهی $ 90^\circ $ میسازد).
2. بدون تغییر شعاع پرگار، سوزن را روی $ B $ گذاشته و کمان دیگری بزنید تا کمان اول را در دو نقطه قطع کند.
3. این دو نقطهی تقاطع را با خطکش به هم وصل کنید. این خط، عمودمنصف $ \overline{AB} $ است.
حالا تصور کنید یک مثلث داریم که سه ضلع دارد: $ \overline{AB} $، $ \overline{BC} $ و $ \overline{CA} $. برای هر یک از این اضلاع میتوانیم یک عمودمنصف رسم کنیم. سؤال بزرگ اینجاست: این سه خط، با هم چه رابطهای دارند؟
بیان قضیه: نقطهی تلاقی مشترک
قضیهی همرسانی عمودمنصفها به زبان ساده میگوید:
یعنی اگر شما عمودمنصف دو ضلع را رسم کنید، حتماً در نقطهای به نام $ O $ یکدیگر را قطع میکنند. جالب اینجاست که عمودمنصف ضلع سوم نیز از همان نقطه$ O $ عبور خواهد کرد. این ویژگی مستقل از نوع مثلث (متساویالاضلاع، متساویالساقین یا مختلفالاضلاع) است.
| نوع مثلث | موقعیت نقطهی برخورد عمودمنصفها ($ O $) | توضیح |
|---|---|---|
| مثلث حادهزاویه³ (همه زوایا کمتر از $ 90^\circ $) | داخل مثلث | نقطهی $ O $ درون ناحیهی محدود به سه ضلع مثلث قرار میگیرد. |
| مثلث قائمالزاویه (یک زاویه برابر $ 90^\circ $) | وسط وتر (ضلع روبرو به زاویه قائمه) | عمودمنصف وتر، از رأس زاویهی قائمه نمیگذرد، اما نقطهی $ O $ دقیقاً وسط آن وتر است. |
| مثلث منفرجهزاویه⁴ (یک زاویه بیشتر از $ 90^\circ $) | خارج مثلث | نقطهی $ O $ در خارج از ناحیهی محدود به سه ضلع مثلث قرار دارد. |
چرا این قضیه درست است؟ (یک استدلال ساده)
برای اثبات این قضیه میتوان از مفهوم مکان هندسی⁵ استفاده کرد. مکان هندسی نقاطی که از دو نقطهی $ A $ و $ B $ به یک فاصله هستند، دقیقاً عمودمنصف پارهخط $ \overline{AB} $ است.
حالا مثلث $ \triangle ABC $ را در نظر بگیرید. عمودمنصف ضلع $ AB $ را رسم میکنیم. هر نقطه روی این خط (مثلاً نقطهی $ O $) از $ A $ و $ B $ فاصلهی یکسانی دارد، یعنی: $ OA = OB $.
به همین ترتیب، عمودمنصف ضلع $ BC $ را رسم میکنیم. هر نقطه روی این خط (مثلاً همان نقطهی $ O $) از $ B $ و $ C $ فاصلهی یکسانی دارد، یعنی: $ OB = OC $.
اگر این دو عمودمنصف همدیگر را در نقطهی $ O $ قطع کنند، آنگاه در این نقطه داریم: $ OA = OB $ و $ OB = OC $. از این دو تساوی نتیجه میگیریم که $ OA = OC $.
اما $ OA = OC $ یعنی نقطهی $ O $ از دو نقطهی $ A $ و $ C $ به یک فاصله است. مکان هندسی چنین نقاطی، دقیقاً عمودمنصف ضلع $ AC $ است. پس نقطهی $ O $ حتماً روی عمودمنصف ضلع سوم نیز قرار دارد. به این ترتیب ثابت شد که هر سه عمودمنصف از یک نقطه میگذرند.
دایرهی محیطی: کاربرد عملی نقطهی برخورد
مهمترین کاربرد این نقطه، رسم دایرهی محیطی¹ مثلث است. دایرهای که از هر سه رأس مثلث میگذرد. چون نقطهی $ O $ از هر سه رأس به یک فاصله است، اگر سوزن پرگار را روی $ O $ بگذاریم و به اندازهی $ OA $ (یا $ OB $ یا $ OC $) شعاع بدهیم، دایرهای رسم میشود که از $ A $، $ B $ و $ C $ میگذرد.
2. پرگار را روی نقطهی $ O $ قرار دهید و شعاع آن را برابر فاصلهی $ O $ تا یکی از رأسها (مثلاً $ A $) تنظیم کنید.
3. دایرهای با این مرکز و شعاع رسم کنید. این دایره از سه رأس مثلث عبور خواهد کرد.
این مفهوم در دنیای واقعی کاربردهای زیادی دارد. برای مثال، اگر سه روستا در مکانهایی غیرهمخط قرار داشته باشند، برای پیدا کردن مکانی که از هر سه روستا به یک فاصله باشد (مثلاً برای احداث یک مرکز امداد مشترک)، کافی است مثلثی با رأسهای این سه روستا رسم کرده و نقطهی برخورد عمودمنصفهای آن را پیدا کنیم. این نقطه دقیقاً محل مورد نظر است.
اشتباهات رایج و پرسشهای مهم
جمعبندی مفهوم همرسانی
پاورقی
¹ دایرهی محیطی (Circumcircle): دایرهای که از همهی رأسهای یک چندضلعی میگذرد. مرکز آن از برخورد عمودمنصفهای اضلاع مثلث بهدست میآید.
² عمودمنصف (Perpendicular Bisector): خطی که یک پارهخط را به دو قسمت مساوی تقسیم کرده و با آن زاویهی قائمه (۹۰ درجه) میسازد.
³ حادهزاویه (Acute): به مثلثی گفته میشود که هر سه زاویهی داخلی آن کمتر از ۹۰ درجه باشد.
⁴ منفرجهزاویه (Obtuse): به مثلثی گفته میشود که یکی از زاویههای داخلی آن بیشتر از ۹۰ درجه باشد.
⁵ مکان هندسی (Locus): مجموعهای از تمام نقاطی که یک خاصیت یا شرط هندسی مشخص را دارا باشند.
⁶ مرکز ثقل (Centroid): نقطهی برخورد سه میانهی مثلث. میانه خطی است که از یک رأس به وسط ضلع مقابل وصل میشود.