متمم یک مجموعه: همهٔ اعضای مرجع که بیرون از مجموعه جا ماندند
زیرنویس: از کلاس اول تا کنکور، ماجرای عضوهای غایب در مجموعه
<!-- خلاصه سئو پسند -->
خلاصه: متمم یک مجموعه، مفهومی کلیدی در نظریهٔ مجموعههاست که تمام عضوهای مجموعهٔ مرجع را شامل میشود، بهجز عضوهایی که در مجموعهٔ اصلی حضور دارند. این ایده در زندگی روزمره (مثل دانشآموزان غایب)، برنامهنویسی (تفاضل لیستها) و آمار (مکمل داده) کاربرد دارد. در این مقاله با زبانی ساده و گامبهگام، از تعریف تا جدول و مثالهای رنگی، متمم را برای همهٔ پایهها توضیح میدهیم.
<!-- بخش اول: زیرموضوع سطح ابتدایی (مدارس ابتدائی) -->
متمم با نگاه کلاسی: چه کسی امروز غایب است؟
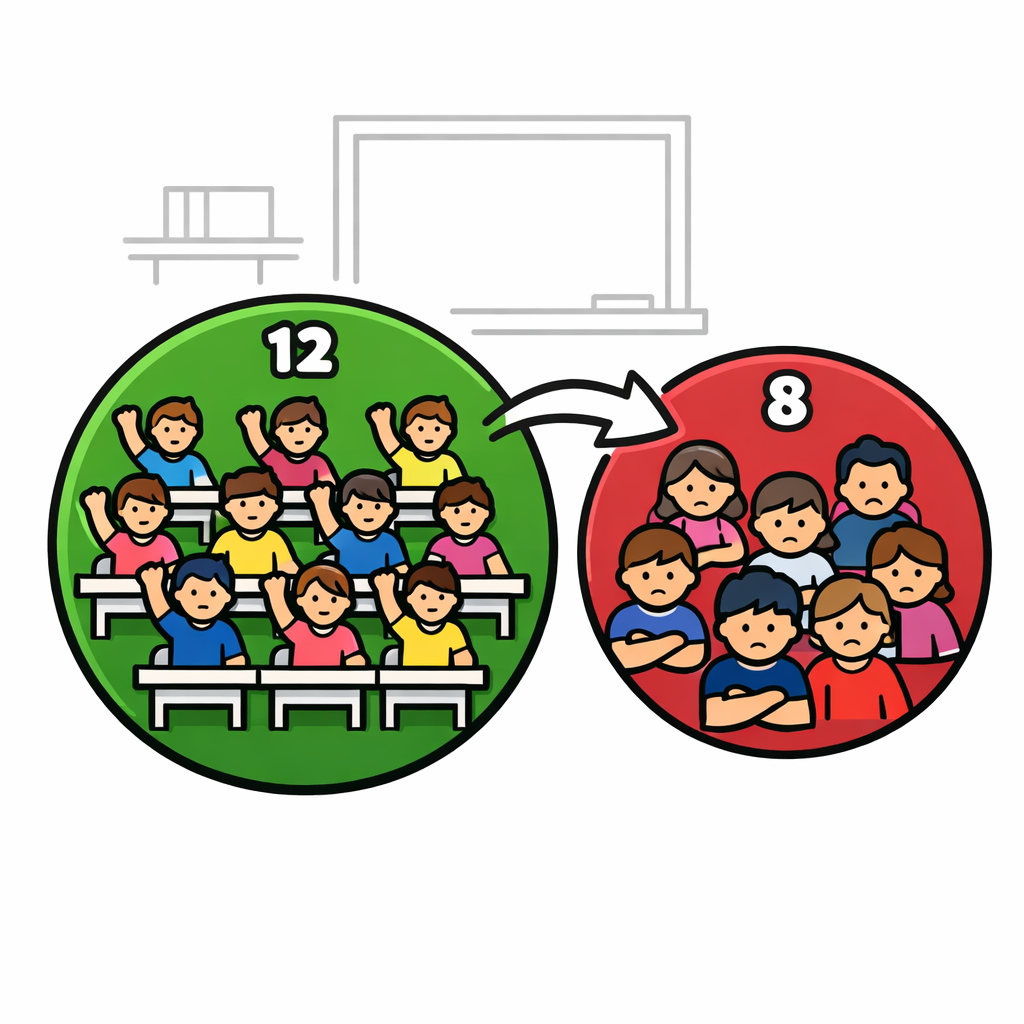
فرض کنید کلاس شما 20 نفر است. این 20 نفر «مجموعهٔ مرجع» هستند. امروز 12 نفر در کلاس حاضرند. مجموعهٔ «حاضرین» یک زیرمجموعه از مرجع است. متمم حاضرین یعنی همان 8 نفری که غایباند. پس متمم یعنی همهٔ عضوهای مجموعهٔ مرجع به جز عضوهای مجموعهٔ مورد نظر.
مثال: مرجع = دانشآموزان کلاس
متمم = غایبان
<!-- جدول زیبا برای نمایش متمم با رنگ بندی -->
| مجموعه | اعضا (تعداد) | اعضای نمونه | متمم (نسبت به مرجع) |
|---|---|---|---|
| دانشآموزان کلاس | 20 نفر | سارا، علی، رضا، … | ———— |
| حاضرین امروز | 12 نفر | سارا، علی، … | غایبان: 8 نفر |
| اعضای تیم فوتبال | 11 نفر | کاپیتان، دروازهبان، … | بازیکنان ذخیره: 7 نفر |
نماد ریاضی و زبان مجموعهها
در ریاضیات معمولاً مجموعهٔ مرجع را با U یا Ω نشان میدهند[1]. اگر مجموعهٔ A را داشته باشیم، متمم آن را به شکلهای زیر مینویسیم:
<!-- فرمول با MathJax در span ltr -->
$A^c$ ،
$A'$ ،
$U \setminus A$ یا
$\overline{A}$.
تعریف رسمی:
$A^c = \{x \in U \mid x \notin A\}$
به زبان فارسی: اعضای متمم، آنهایی از مجموعهٔ مرجع هستند که در Aنیستند. مثلاً اگر $U = \{۱,۲,۳,۴,۵,۶\}$ و $A = \{۲,۴,۶\}$ آنگاه متمم $A^c = \{۱,۳,۵\}$ خواهد بود.
<!-- باکس نکته طلایی -->
? نکته: متمم همیشه به یک مجموعهٔ مرجع وابسته است. اگر مرجع عوض شود، متمم هم کاملاً تغییر میکند. برای همین همیشه اول بپرسید «مرجع چیست؟»
<!-- بخش سوم: زیرموضوع سطح دبیرستان (جبر مجموعهها، قوانین دمورگان) -->
جبر متمم: اجتماع، اشتراک و قوانین دمورگان
وقتی با چند مجموعه کار میکنیم، متممها رابطههای زیبایی پیدا میکنند. این روابط در ریاضی دبیرستان بسیار مهم هستند:
- $(A^c)^c = A$ (متممِ متمم، خود مجموعه است)
- $U^c = \varnothing$ و $\varnothing^c = U$ (متمم مرجع تهی است و برعکس)
- قانون دمورگان[2]: $(A \cup B)^c = A^c \cap B^c$ و $(A \cap B)^c = A^c \cup B^c$
مثال با اعداد: اگر $U=\{۱,۲,۳,۴,۵\}$ و $A=\{۱,۲\}$ و $B=\{۲,۳\}$ باشد، $(A\cup B)^c = \{۱,۲,۳\}^c = \{۴,۵\}$ و از طرفی $A^c=\{۳,۴,۵\}$ و $B^c=\{۱,۴,۵\}$ و اشتراکشان $\{۴,۵\}$ است. قانون دمورگان دقیقاً برقرار است.
<!-- بخش چهارم: کاربرد عملی و مثال عینی (H3 با عنوان هماهنگ) -->
کاربرد در فروشگاه: متمم سبد خرید
فروشگاه اینترنتی «گاما مارکت» را تصور کنید. مرجع = ۱۰۰ قلم کالا. مشتری ۱۲ کالا را به سبد خرید اضافه کرده است. مدیر فروشگاه میخواهد بداند چه کالاهایی را هنوز مشتری ندیده (یا نخریده) است. متمم سبد خرید (نسبت به کل کالاها) همان ۸۸ کالای باقیمانده است. با این تحلیل میتوان پیشنهاد «شگفتانگیز» برای کالاهای متمم طراحی کرد.
مثال زنده
در یک نظرسنجی از ۳۰۰ خانوار، ۱۲۰ خانوار تلویزیون برند A دارند. متمم این مجموعه یعنی ۱۸۰ خانوار که برند A ندارند (ممکن است برند دیگر داشته باشند یا اصلاً تلویزیون نداشته باشند). این عدد برای بازاریابان بسیار ارزشمند است.
<!-- جدول دوم: کاربرد در منطق و احتمال -->
| پیشامد | احتمال | متمم | احتمال متمم |
|---|---|---|---|
| آوردن ۶ با تاس | $\frac{۱}{۶}$ | نیاوردن ۶ | $\frac{۵}{۶}$ |
| بارانی بودن فردا | $۰.۳$ | بارانی نبودن | $۰.۷$ |
اشتباهات رایج و پرسشهای مهم
❓ سوال ۱: آیا متمم همیشه وجود دارد؟
پاسخ: خیر! متمم همیشه به یک مجموعهٔ مرجع نیاز دارد. اگر مرجع تعریف نشده باشد، متمم معنایی ندارد. مثل این است که بگویید «غایبان» بدون اینکه معلوم باشد کلاس چند نفر است.
پاسخ: خیر! متمم همیشه به یک مجموعهٔ مرجع نیاز دارد. اگر مرجع تعریف نشده باشد، متمم معنایی ندارد. مثل این است که بگویید «غایبان» بدون اینکه معلوم باشد کلاس چند نفر است.
❓ سوال ۲: تفاوت متمم و تفاضل دو مجموعه چیست؟
پاسخ: متمم یعنی $U-A$ اما تفاضل دو مجموعه $A-B$ عضوهایی از A است که در B نیستند. متمم یک حالت خاص از تفاضل است وقتی مجموعهٔ اول، مجموعهٔ مرجع باشد.
پاسخ: متمم یعنی $U-A$ اما تفاضل دو مجموعه $A-B$ عضوهایی از A است که در B نیستند. متمم یک حالت خاص از تفاضل است وقتی مجموعهٔ اول، مجموعهٔ مرجع باشد.
❓ سوال ۳: چرا گاهی متمم را با $\overline{A}$ و گاهی با $A^c$ نشان میدهند؟
پاسخ: هر دو نماد رایج هستند. $A^c$ مخفف complement و $\overline{A}$ در نظریه مجموعهها و آمار کاربرد دارد. هر دو به یک معنا هستند.
پاسخ: هر دو نماد رایج هستند. $A^c$ مخفف complement و $\overline{A}$ در نظریه مجموعهها و آمار کاربرد دارد. هر دو به یک معنا هستند.
? جمعبندی: متمم یک مجموعه، تمام عضوهای مجموعهٔ مرجع را در بر میگیرد به جز عضوهای خود مجموعه. این مفهوم ساده در همهٔ سطوح ریاضی، از شمارش دانشآموزان غایب تا قوانین دمورگان و احتمال، کاربرد دارد. همیشه به یاد داشته باشید که متمم بدون «مجموعهٔ مرجع» تعریف نمیشود و رابطههای مهمی مثل $(A^c)^c = A$ ستون فقرات استدلالهای ریاضی را تشکیل میدهند.
<!-- پاورقی (H3) با تعریف واژههای نامأنوس -->
پاورقی
[1] مجموعهٔ مرجع (Universal set): مجموعهای که همهٔ اعضای مورد بحث را در بر دارد.
[2] قوانین دمورگان (De Morgan's laws): روابطی بین متمم اجتماع و اشتراک که به افتخار ریاضیدان بریتانیایی آگوستوس دمورگان نامگذاری شده است.
واژهٔ «متمم» (Complement) در ریاضی به معنای تکمیلکننده و تمامکننده است.
<!-- تراشههای کلمات کلیدی (بدون هدینگ) -->
[2] قوانین دمورگان (De Morgan's laws): روابطی بین متمم اجتماع و اشتراک که به افتخار ریاضیدان بریتانیایی آگوستوس دمورگان نامگذاری شده است.
واژهٔ «متمم» (Complement) در ریاضی به معنای تکمیلکننده و تمامکننده است.
#متمم_مجموعه
#مجموعه_مرجع
#قانون_دمورگان
#احتمال_متمم
#ریاضی_دبیرستان
