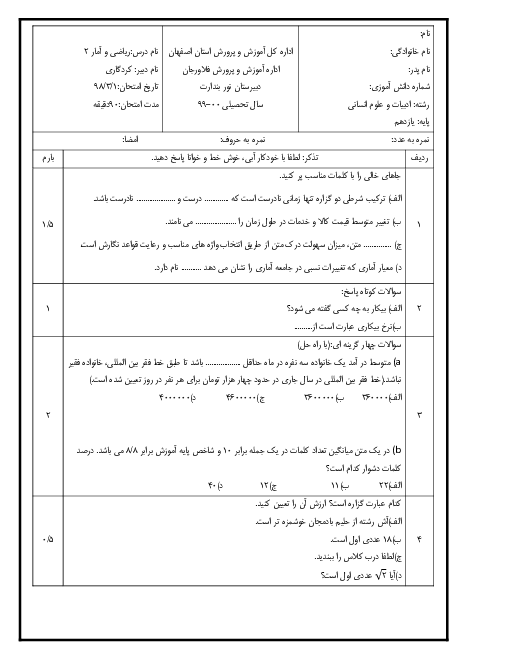
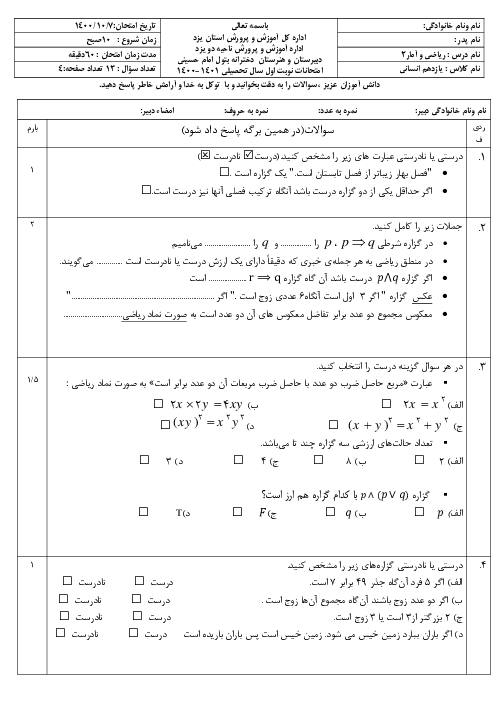
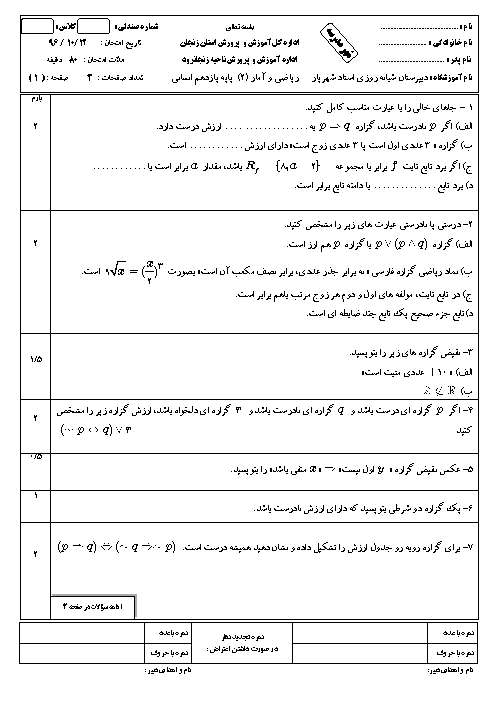
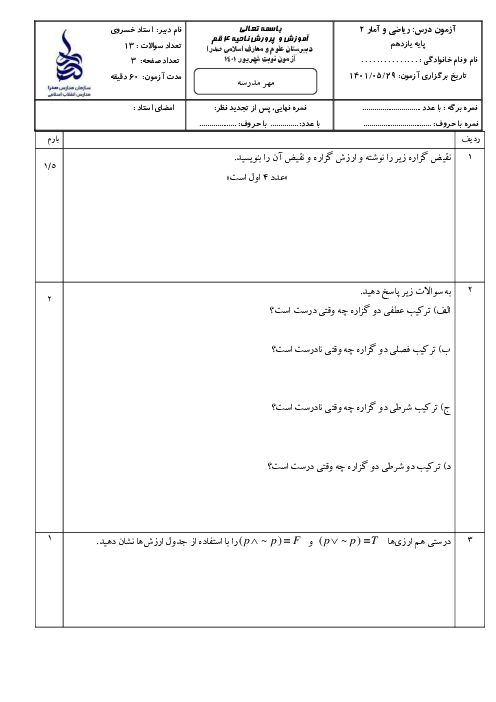
به بررسی تک‌تک گزينه‌ها می‌پردازيم،داريم: 

$1)-3\lt x\lt -1\Rightarrow \frac{-3}{3}\lt \frac{x}{3}\lt \frac{-1}{3}\Rightarrow -1\lt \frac{x}{3}\lt \frac{-1}{3}\Rightarrow \frac{+1}{3}\lt \frac{-x}{3}\lt 1$

$\Rightarrow 2+\frac{1}{3}\lt 2-\frac{x}{3}\lt 2+1\Rightarrow 2\lt \frac{7}{3}\lt 2-\frac{x}{3}\lt 3\Rightarrow f(x)=\left[ 2-\frac{x}{3} \right]=2$

$2)-3\lt x\lt -1\Rightarrow \frac{-3}{4}\lt \frac{x}{4}\lt \frac{-1}{4}\Rightarrow -1\lt \frac{-3}{4}\lt \frac{x}{4}\lt \frac{-1}{4}\lt 0\Rightarrow -1\lt \frac{x}{4}\lt 0$

$\Rightarrow g(x)=\left[ \frac{x}{4} \right]=-1$

$3)-3\lt x\lt -1\Rightarrow \frac{-3}{3}\lt \frac{x}{3}\lt \frac{-1}{3}\Rightarrow -1\lt \frac{x}{3}\lt \frac{-1}{3}$

$\Rightarrow -1-1\lt \frac{x}{3}-1\lt \frac{-1}{3}-1\Rightarrow -2\lt \frac{x}{3}-1\lt \frac{-4}{3}\lt -1\Rightarrow -2\lt \frac{x}{3}-1\lt -1$

$\Rightarrow k(x)=\left[ \frac{x}{3}-1 \right]=-2$

$4)-3\lt x\lt -1\Rightarrow -3+1\lt x+1\lt -1+1\Rightarrow -2\lt x+1\lt 0$

$\Rightarrow \frac{-2}{2}\lt \frac{x+1}{2}\lt \frac{0}{2}\Rightarrow -1\lt \frac{x+1}{2}\lt 0\Rightarrow h(x)=\left[ \frac{x+1}{2} \right]=-1$