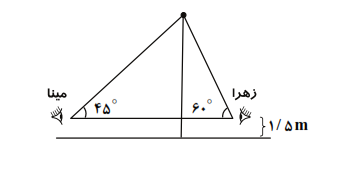
فرض میکنیم $A$ و $B$ چشمان زهرا و مینا و $C$ سر تیرک باشد، داریم:
$\cot {{60}^{{}^\circ }}=\frac{AH}{CH}\,\Rightarrow AH=CH\times Cot{{60}^{{}^\circ }}\Rightarrow AH=\frac{\sqrt{3}}{3}CH$
$\cot \,{{45}^{{}^\circ }}=\frac{BH}{CH}\Rightarrow BH=CH\times \cot {{45}^{{}^\circ }}\Rightarrow BH=CH$
با جمع دو رابطهی بالا داریم:
$\underbrace{AH+BH}_{AB}=CH+\frac{\sqrt{3}}{3}+CH=CH(1+\frac{\sqrt{3}}{3})=\frac{3+\sqrt{3}}{3}CH$
بنابراین:
$27+9\sqrt{3}=\frac{3+\sqrt{3}}{3}CH\Rightarrow CH=\frac{3(27+9\sqrt{3})}{3+\sqrt{3}}=\frac{3\times 9(3+\sqrt{3})}{3+\sqrt{3}}=27$
ارتفاع تیرک با اضافه کردن طول قد به این مقدار حاصل میشود. پس طول تیرک برابر $27+1/5=28/5$ است.