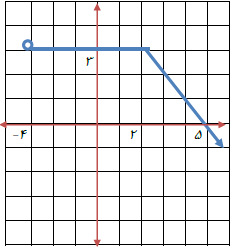
برای به دست آوردن ضابطه تابع باید دامنه تابع را از روی محور طول‌ها به دست بیاوریم سپس ضابطه هر کدام از دامنه‌ها را پیدا می‌کنیم. قسمت اول نمودار یک تابع ثابت و قسمت دوم یک تابع خطی است. بنابراین ضابطه اول به راحتی به دست می‌آید. یعنی:

$f(x) = \left\{ {\begin{array}{*{20}{c}}  3&{ - 4 < x \leqslant 2} \\   ?&? \end{array}} \right.$

برای پیدا کردن ضابطه دوم نقاط ابتدا و انتهای خط را مشخص می‌کنیم و شیب خط را به کمک دو نقطه مشخص می‌کنیم:

$(2,3),(5,0)$

شیب خط را به کمک این دو نقطه به دست می‌آوریم:

$m = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \frac{{0 - 3}}{{5 - 2}} = \frac{{ - 3}}{3} =  - 1$

به کمک یک نقطه (که از نقطه دوم استفاده می‌کنیم) و شیب خط معادله خط را به دست می‌آوریم که همان ضابطه تابع می‌شود.

$\eqalign{
  & y = m(x - {x_1}) + {y_1} \to y =  - 1(x - 5) + 0 \to y =  - x + 5 + 0  \cr 
  &  \to y =  - x + 5 \to f(x) =  - x + 5 \cr} $

پس تابع دو ضابطه‌ای به صورت زیر خواهد بود:

$f(x) = \left\{ {\begin{array}{*{20}{c}} 3&{ - 4 < x \leqslant 2} \\   { - x + 5}&{2 \leqslant x} \end{array}} \right.$