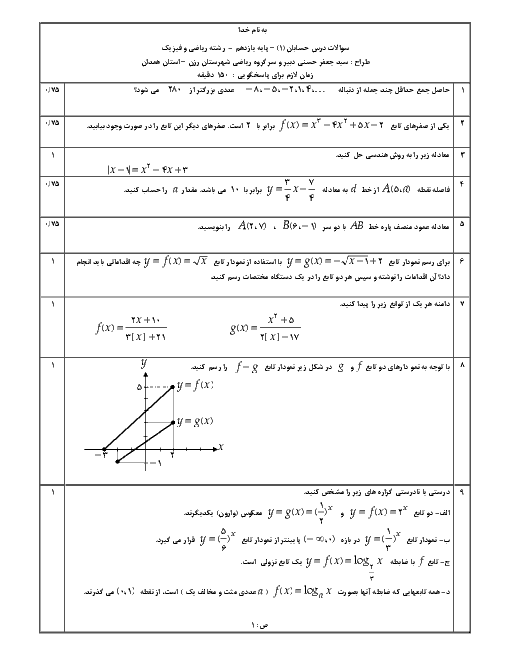
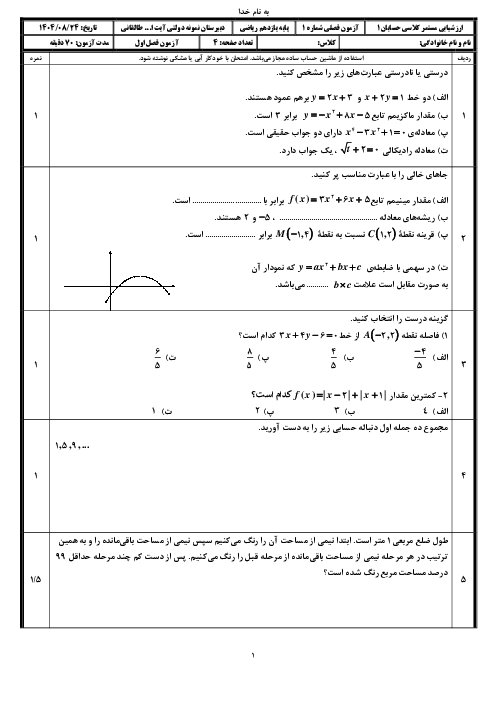
نکته: $\operatorname{Sin}(\frac{\pi }{2}-\alpha )=\operatorname{Cos}\alpha $

نکته: ${{\operatorname{Sin}}^{2}}\alpha +{{\operatorname{Cos}}^{2}}\alpha =1$

با توجه به فرض سؤال $\alpha +\beta =\frac{\pi }{2}$، بنابراین $\beta =\frac{\pi }{2}-\alpha $، پس:

$\operatorname{Sin}\beta =\operatorname{Sin}(\frac{\pi }{2}-\alpha )=\operatorname{Cos}\alpha $

برای به‌دست آوردن مقدار $\operatorname{Cos}\alpha $ با استفاده از مقدار $\operatorname{Sin}\alpha $ داريم: 

${{\operatorname{Sin}}^{2}}\alpha +{{\operatorname{Cos}}^{2}}\alpha =1\Rightarrow {{(\frac{-24}{25})}^{2}}+{{\operatorname{Cos}}^{2}}\alpha =1\Rightarrow {{\operatorname{Cos}}^{2}}\alpha =1-\frac{576}{625}\Rightarrow {{\operatorname{Cos}}^{2}}\alpha =\frac{49}{625}$

چون $\alpha $ در ربع سوم است، پس: $\operatorname{Cos}\alpha =-\frac{7}{25}$، بنابراین:

$\operatorname{Sin}\beta =-\frac{7}{25}$