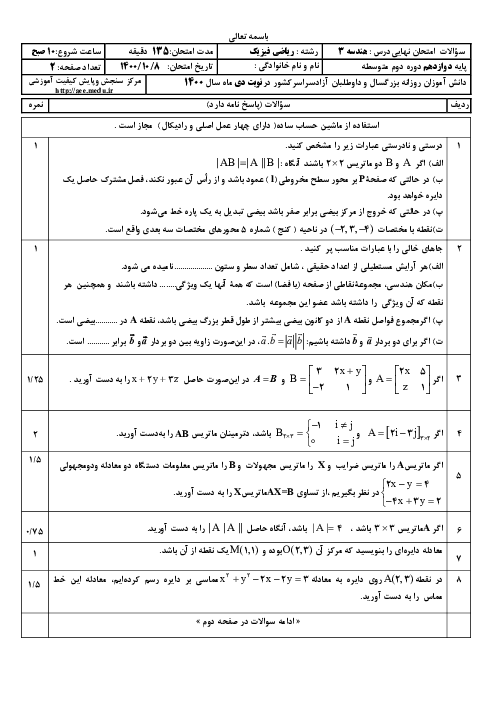
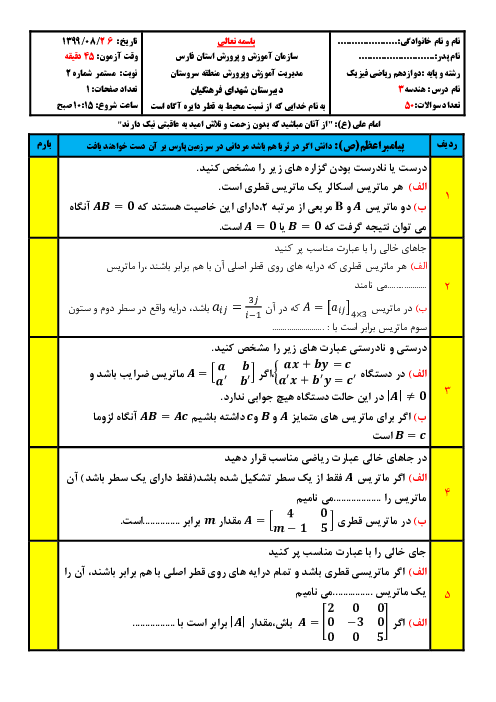
ابتدا دستگاه را حل می‌کنیم:

$\left\{ \begin{matrix} 3x-y=3  \\ x+y=5  \\ \end{matrix} \right.\xrightarrow{+}4x=8\Rightarrow x=2,y=3$

$\left[ \begin{matrix} \begin{matrix} 2  \\ -1  \\ \end{matrix} & \begin{matrix} 3  \\ 4  \\ \end{matrix}  \\ \end{matrix} \right]\left[ \begin{matrix} x+y  \\ x-y  \\ \end{matrix} \right]=\left[ \begin{matrix} a+1  \\ a+b  \\ \end{matrix} \right]\Rightarrow $$\left[ \begin{matrix} \begin{matrix} 2  \\ -1  \\ \end{matrix} & \begin{matrix} 3  \\ 4  \\ \end{matrix}  \\ \end{matrix} \right]\left[ \begin{matrix} 5  \\ -1  \\ \end{matrix} \right]=\left[ \begin{matrix} a+1  \\ a+b  \\ \end{matrix} \right]\Rightarrow $

$\Rightarrow \left[ \begin{matrix} a+1  \\ a+b  \\ \end{matrix} \right]=\left[ \begin{matrix} 7  \\ -9  \\ \end{matrix} \right]\Rightarrow \left\{ \begin{matrix} a+1=7\Rightarrow a=6  \\ a+b=-9\Rightarrow 6+b=-9\Rightarrow b=-15  \\ \end{matrix} \right.$