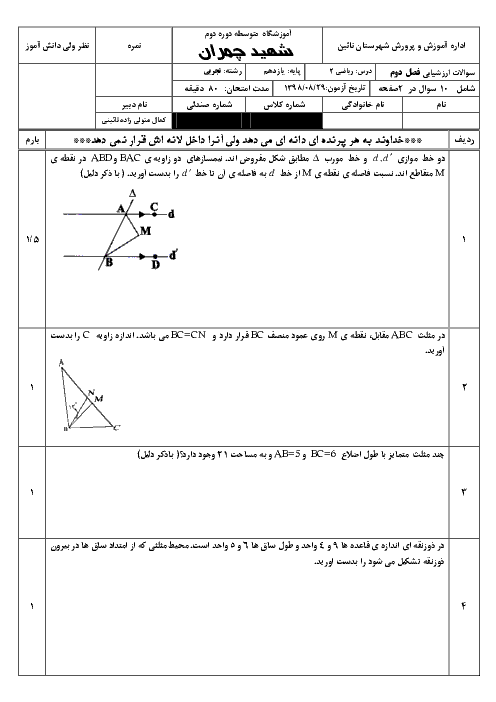
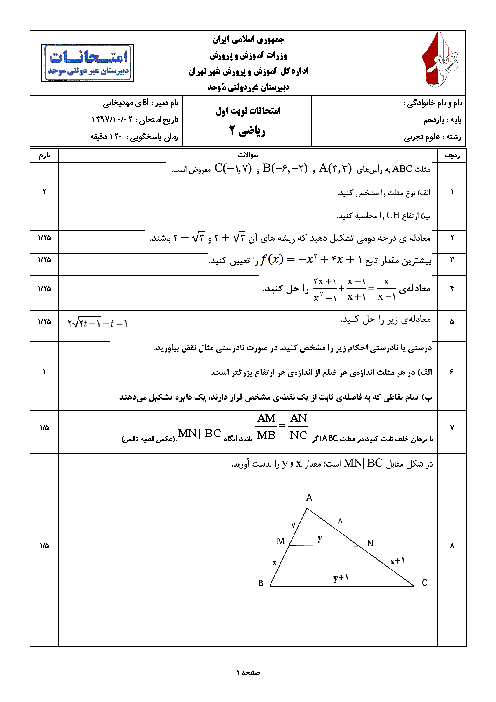
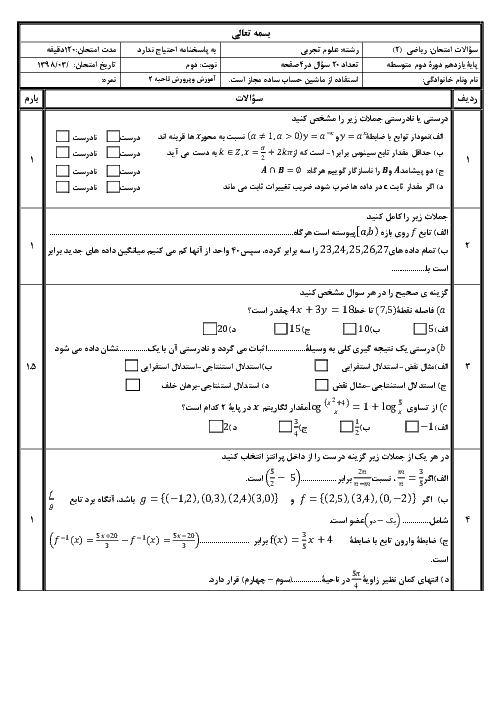
مقادیر b و a را چنان تعیین کنید که تابع زیر در نقطهٔ $x = - 1$ پیوسته باشد.
$f(x) = \left\{ \begin{gathered}
- 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x \lt - 1 \hfill \\
ax + b\,\,\,\,\,\,\,\,x = - 1 \hfill \\
{x^2} - b\,\,\,\,\,\,\,\,x \gt - 1 \hfill \\
\end{gathered} \right.$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...