کدام گزینه صحیح است؟ | ریاضی (3) دوازدهم شماره 68828

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

درس 1: توابع چند جمله‌ای- توابع صعودی و نزولی ریاضی (3) دوازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

کدام گزینه صحیح است؟

1 )

نمودار تابع $f(x)=-{{x}^{3}}-2$ از ناحیهٔ دوم نمی‌گذرد.

2 )

نمودار تابع $f(x)={{(x+2)}^{3}}$ از ناحیهٔ دوم نمی‌گذرد.

3 )

نمودار تابع $f(x)=-{{(x-2)}^{3}}$ از ناحیهٔ سوم نمی‌گذرد.

4 )

دو تابع $f(x)={{x}^{3}}$ و $g(x)={{x}^{2}}$ در محدودهٔ $x\gt 0$ نقطهٔ برخوردی ندارند.

نمایش پاسخ

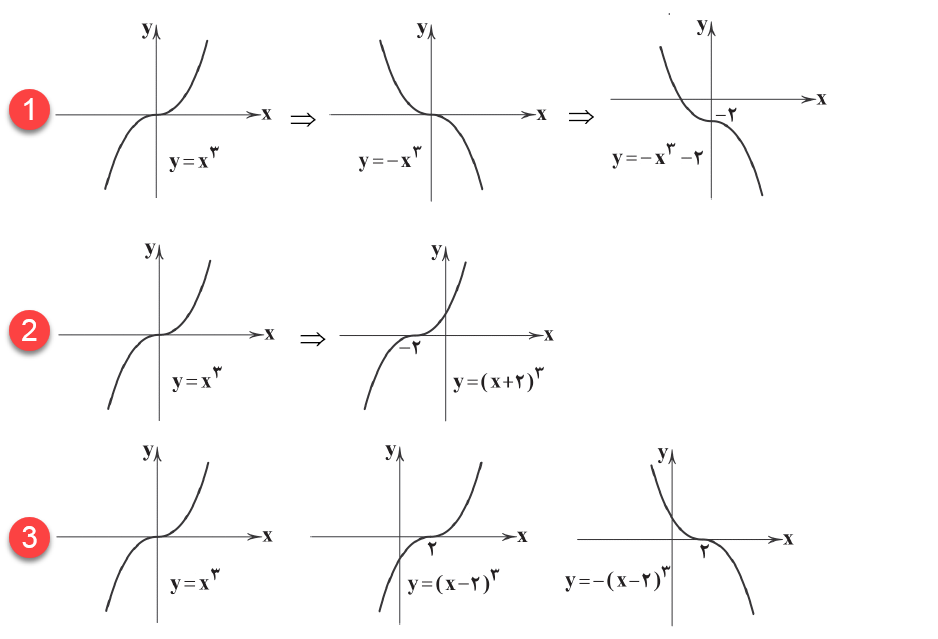
برای رسم نمودار $-{{x}^{3}}-2$ به‌ترتیب توابع ${{x}^{3}}$ ، $-{{x}^{3}}$ و $-{{x}^{3}}-2$ را رسم می‌کنیم.

ملاحظه می‌کنید که تابع $-{{x}^{3}}-2$ از ناحیهٔ اول نمی‌گذرد.

2) برای رسم ${{(x+2)}^{3}}$ ابتدا ${{x}^{3}}$ سپس ${{(x+2)}^{3}}$ را رسم می‌کنیم.

ملاحظه می‌کنید که تابع ${{(x+2)}^{3}}$ از ناحیهٔ چهارم عبور نمی‌کند.

3) برای رسم $-{{(x-2)}^{3}}$ به‌ترتیب توابع ${{x}^{3}}$، ${{(x-2)}^{3}}$ و $-{{(x-2)}^{3}}$ را رسم می‌کنیم:

ملاحظه می‌کنید که تابع $-{{(x-2)}^{3}}$ از ناحیهٔ سوم عبور نمی‌کند.

4) ضمناً اگر دو تابع ${{x}^{3}}$ و ${{x}^{2}}$ را رسم کنیم، در دو نقطهٔ $x=1$ و $x=0$ متقاطع‌اند که برای $x$ های مثبت، $x=1$ قابل قبول است. البته می‌توان بدون رسم هم نقاط برخورد را محاسبه کرد.

${{x}^{3}}={{x}^{2}}\Rightarrow {{x}^{3}}-{{x}^{2}}=0\Rightarrow {{x}^{2}}(x-1)=0\xrightarrow{x\gt 0}x=1$