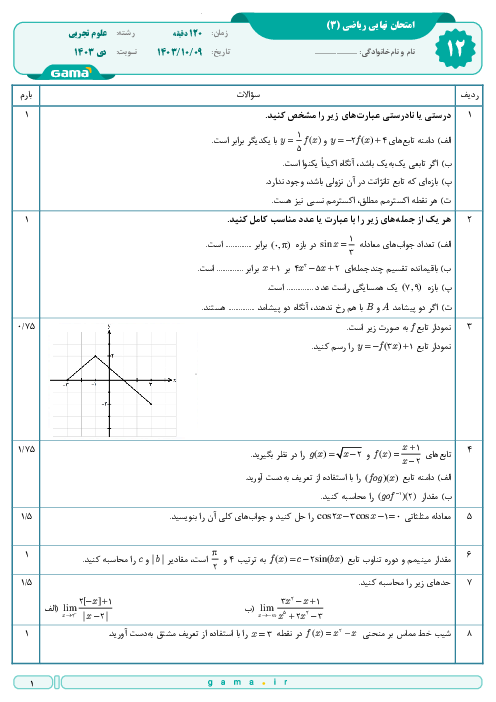
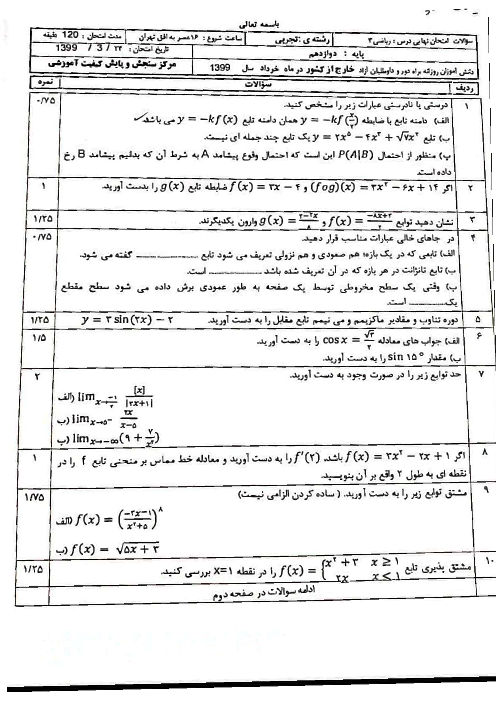
درس 1: توابع چند جمله‌ای- توابع صعودی و نزولی
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
اگر در تابع اکیداً صعودی $f$ داشته باشیم $f({{a}^{2}}+\left| a \right|+1)>f({{a}^{2}}-\left| a \right|+3)$، مجموعه مقادیر قابل‌قبول برای $a$ کدام است؟
$\left| a \right|\gt 1$
2 )
$\left| a \right|\lt 1$
3 )
$\varnothing $
4 )
$\mathbb{R}$
پاسخ تشریحی :
تحلیل ویدئویی تست
مصطفی الفت 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...