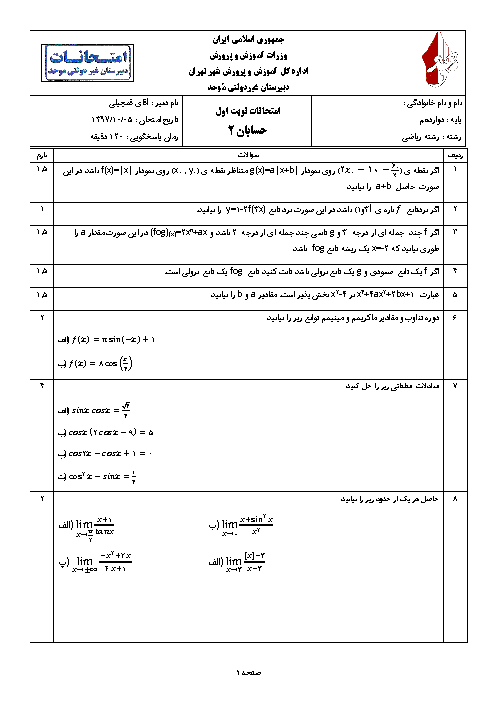
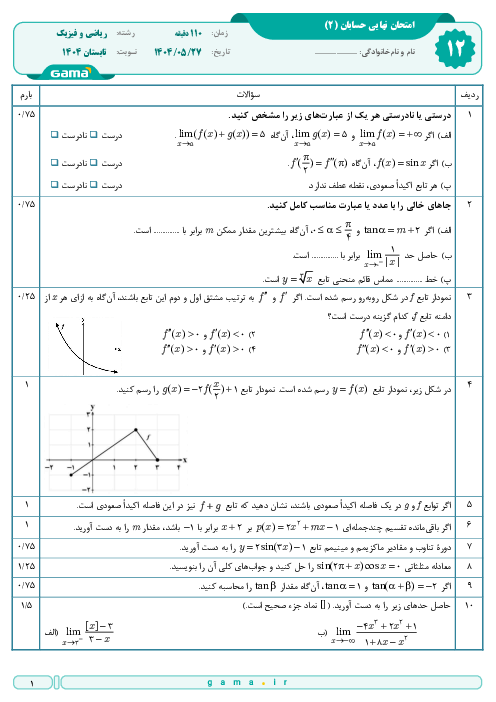
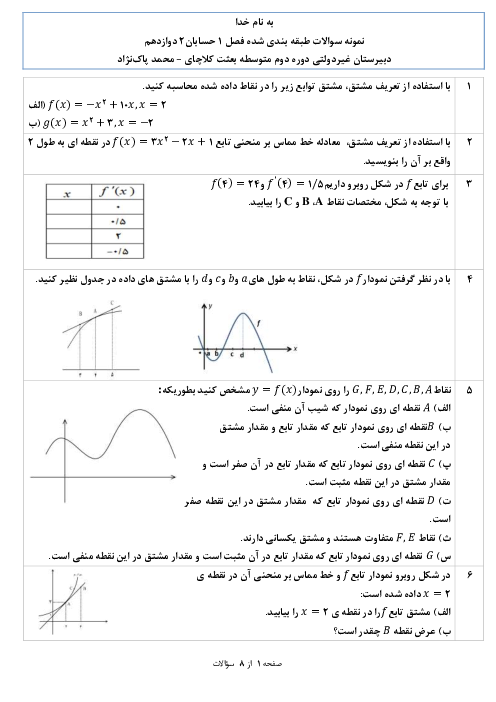
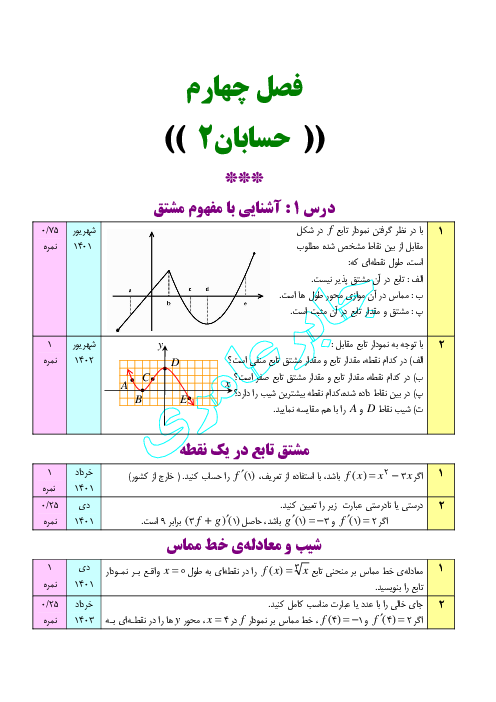
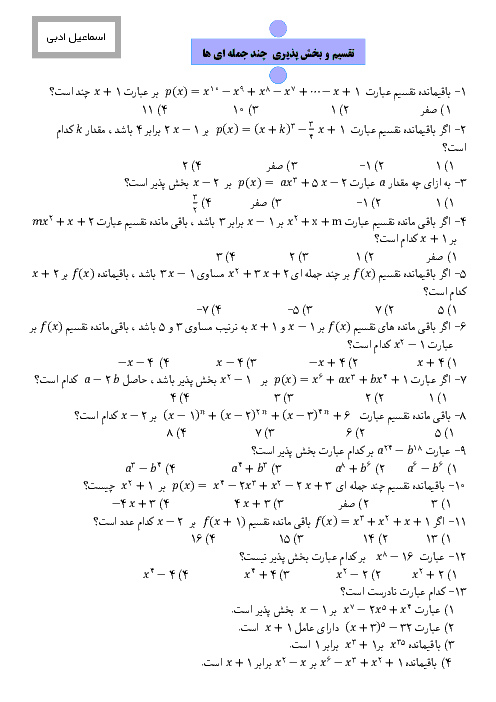داریم:

$f(x)=\left\{ \begin{matrix}    a{{x}^{2}}+bx+c\,\,\,\,,\,\,\,\,\left| x \right|\le 1  \\    x+\left| x \right|\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\left| x \right| \gt 1  \\ \end{matrix} \right.$

$\Rightarrow f(x)=\left\{ \begin{matrix}    0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,x \lt -1  \\    a{{x}^{2}}+bx+c\,\,\,\,,\,\,\,\,-1\le x\le 1  \\    2x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,x \gt 1  \\ \end{matrix} \right.$

$\Rightarrow {f}'(x)\left\{ \begin{matrix}    0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,x \lt -1  \\    2ax+b\,\,\,\,,\,\,\,\,-1 \lt x \lt 1  \\    2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,x \gt 1  \\ \end{matrix} \right.$ 

برای این‌که $f$ روی $g$ مشتق‌‌پذیر باشد، لازم است در نقاط $x=\pm 1$ مشتق‌پذیر و در نتیجه پیوسته نیز باشد.

$(1)$        $a+b=c=2$ $\Rightarrow $ شرط پیوستگی در $x=1$

$(2)$       $a-b+c=0$ $\Rightarrow $ شرط پیوستگی در $x=-1$ 

$(3)$      $(1),(2)\Rightarrow a+c=1$ 

$(4)$      $2a+b=2$ $\Rightarrow $ شرط مشتق‌پذیری در $x=1$ 

$(5)$      $-2a+b=0$ $\Rightarrow $ شرط مشتق‌پذیری در $x=-1$ 

$(4),(5)\Rightarrow b=1,a=\frac{1}{2}\xrightarrow{(3)}c=\frac{1}{2}\Rightarrow 2a+b+4c=4$