از طرف هوا، نيروی شناوری به طرف بالا و از طرف زمين نيروی وزن به طرف پايين بر بالن وارد می‌شود.

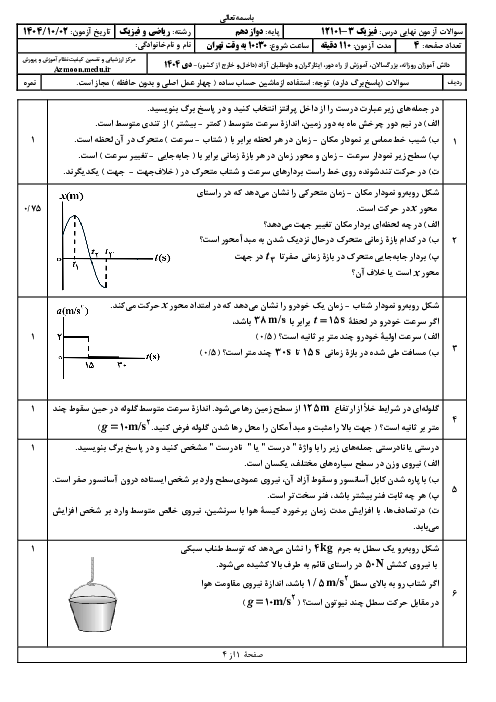
اگر جرم اوليه‌ی بالن $M$ فرض شود، با استفاده از قانون دوم نيوتون در حالت اول داريم:

${{F}_{net}}=Ma\Rightarrow Mg-{{F}_{b}}=Ma\Rightarrow {{F}_{b}}=M\left( g-a \right)\left( * \right)$ 

چون اندازه‌ی نيروی شناوری ثابت فرض شده است، در حالت دوم با كاهش جرم بالن به اندازه‌ی $m$، بالن با شتاب ثابت $a$ و به صورت تندشونده بالا خواهد رفت. با استفاده از قانون دوم نيوتون خواهيم داشت:

${{{F}'}_{net}}=\left( M-m \right)a\Rightarrow {{F}_{b}}-\left( M-m \right)g=\left( M-m \right)a\xrightarrow{\left( * \right)}Mg-Ma-Mg=Ma-ma\Rightarrow m=\frac{2Ma}{g+a}$ 

بنابراين درصد تغييرات جرم بالن برابر است با:

$\frac{m}{M}\times 100=\frac{2a}{g+a}\times 100=\frac{200a}{g+a}$