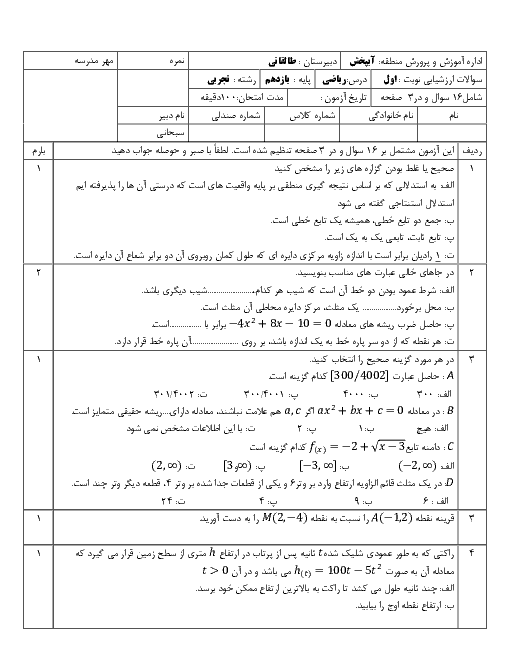
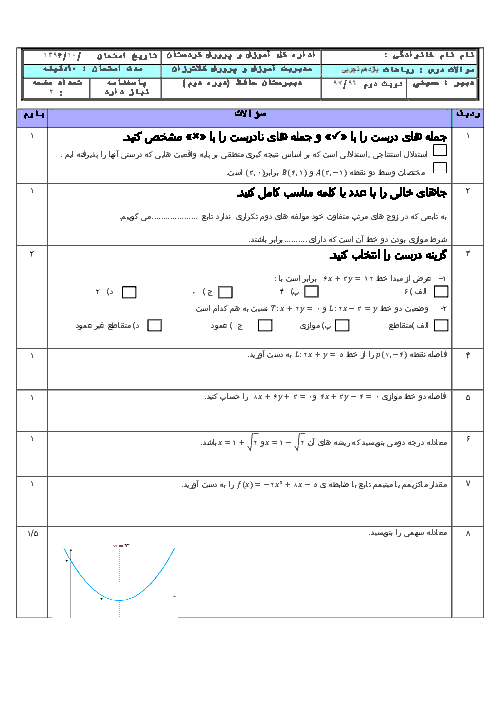
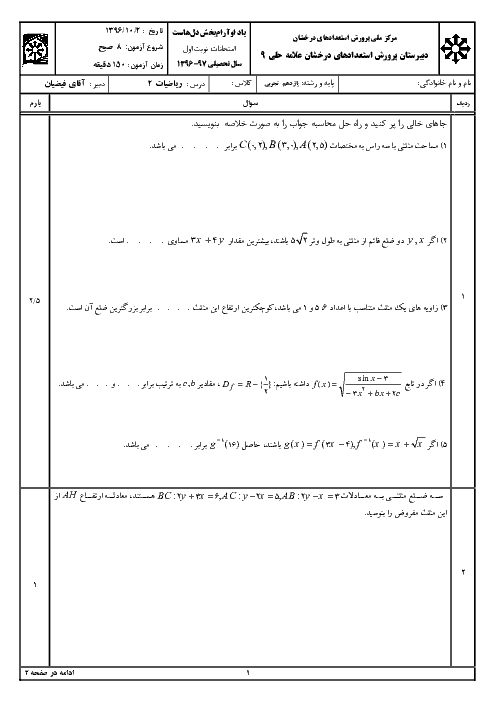
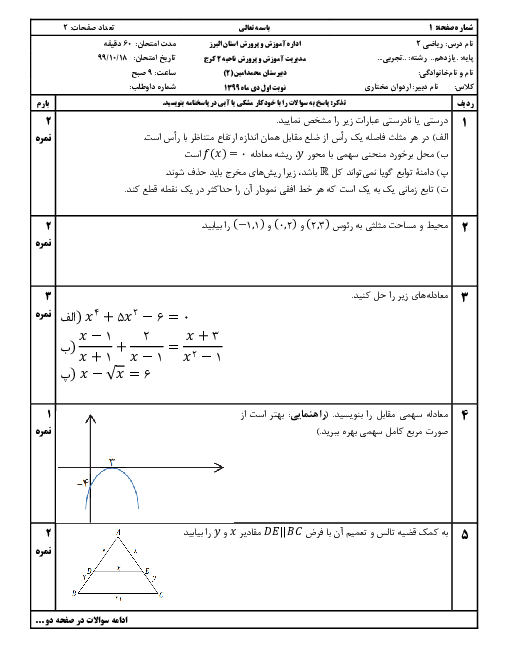
درس 2: معادلهٔ درجهٔ دوم و تابع درجه 2
ریاضی (2)
یازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
قرار است در کنار یک رودخانه، محوطهای مستطیل شکل ایجاد کنیم. برای این کار لازم است سه ضلع محوطه نرده کشی شود. اگر تنها هزینۀ 100 متر نرده را در اختیار داشته باشیم و بخواهیم مساحت این مستطیل بیشترین مقدار ممکن گردد، مقدار x کدام است؟