درس 1: مفاهیم اولیه و زاویهها در دایره
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
در شکل زیر O مرکز دایره است. ثابت کنید؛ اندازهٔ زاویهٔ محاطی $\hat M$، برابر با نصف اندازهٔ کمان مقابل به آن زاویه است.
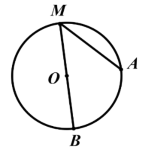
پاسخ تشریحی :
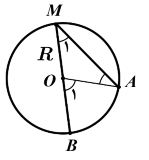
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...