نکته: حاصل حد زیر در صورت وجود برابر با شیب نیم‌مماس چپ تابع $f$ در نقطه‌ی $x=a$ است.

شیب نیم‌مماس چپ $={{{f}'}_{-}}(a)=\underset{x\to {{a}^{-}}}{\mathop{lim}}\,\frac{f(x)-f(a)}{x-a}$ 

نکته: حاصل حد زیر در صورت وجود برابر با شیب نیم‌مماس راست تابع $f$ در نقطه‌ی $x=a$ است.

شیب نیم‌مماس راست $={{{f}'}_{+}}(a)=\underset{x\to {{a}^{+}}}{\mathop{lim}}\,\frac{f(x)-f(a)}{x-a}$ 

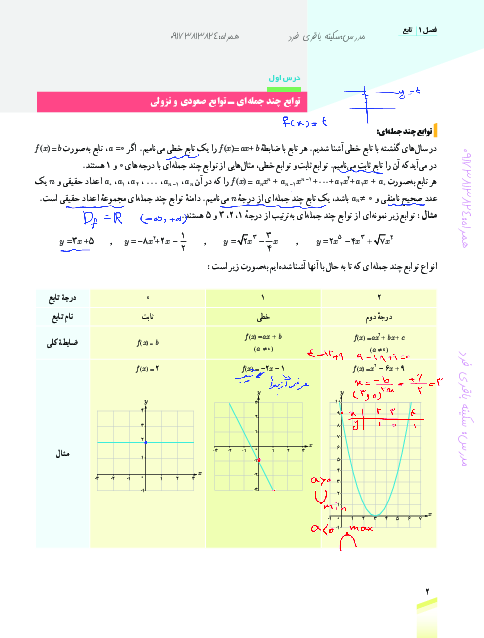
با توجه به نکات داریم:

$f(x)=m({{x}^{2}}-4)\left[ x \right]\,\,,\,\,f(-2)=0$ 

${{{f}'}_{-}}(-2)=\underset{x\to -{{2}^{-}}}{\mathop{\lim }}\,\frac{f(x)-f(-2)}{x-(-2)}=\underset{x\to -{{2}^{-}}}{\mathop{\lim }}\,\frac{m({{x}^{2}}-4)\left[ x \right]-0}{x+2}$

$=\underset{x\to -{{2}^{-}}}{\mathop{\lim }}\,\frac{m(x+2)(x-2)\left[ x \right]}{x+2}=\underset{x\to -{{2}^{-}}}{\mathop{\lim }}\,m(x-2)\left[ x \right]=m(-4)(-3)=12m$ 

${{{f}'}_{+}}(-2)=\underset{x\to -{{2}^{+}}}{\mathop{\lim }}\,\frac{f(x)-f(-2)}{x-(-2)}=\underset{x\to -{{2}^{+}}}{\mathop{\lim }}\,\frac{m(x+2)(x-2)\left[ x \right]}{x+2}$

$=\underset{x\to -{{2}^{+}}}{\mathop{\lim }}\,m(x-2)\left[ x \right]=m(-4)(-2)=8m$

مطابق فرض مجموع این دو مقدار $-40$ است، پس داریم:

$12m+8m=-40\Rightarrow 20m=-40\Rightarrow m=-2$