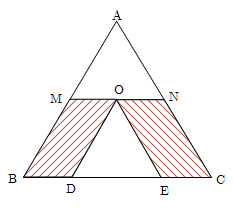
$\begin{matrix}
AM=MB \\
AN=NC \\
\end{matrix}\Rightarrow MN=\frac{1}{2}BC\Rightarrow S\,\,{}_{\overset{\Delta }{\mathop{AMN}}\,}=\frac{1}{4}S\,{}_{\overset{\Delta }{\mathop{ABC}}\,}$

$\begin{matrix}
OD\parallel AB\Rightarrow \overset{\wedge }{\mathop{{{D}_{1}}}}\,={{\overset{\wedge }{\mathop{M}}\,}_{1}} \\
OE\parallel AC\Rightarrow \overset{\wedge }{\mathop{{{E}_{1}}=}}\,\overset{\wedge }{\mathop{{{N}_{1}}}}\, \\
\end{matrix}\Rightarrow \overset{\wedge }{\mathop{O}}\,=\overset{\wedge }{\mathop{A}}\,$

بنابراین: دو چهارضلعی $ONCE$ و $OMBD$ متوازی‌الاضلاع هستند.

در نتیجه:

$\begin{matrix}
OE=NC=AN \\
OD=MB=AM \\
\end{matrix}$

بنابراین: دو مثلث $\overset{\Delta }{\mathop{AMN}}\,$ و $\overset{\Delta }{\mathop{ODE}}\,$ هم نهشتند.

$S\,{}_{\overset{\Delta }{\mathop{ODE}}\,}=S{{\,}_{\overset{\Delta }{\mathop{AMN}}\,}}=\frac{1}{4}S{{\,}_{\overset{\Delta }{\mathop{ABC}}\,}}$

$S{{\,}_{\overset{\Delta }{\mathop{ODE}}\,}}=S{{\,}_{\overset{\Delta }{\mathop{AMN}}\,}}\,=\frac{1}{4}S{{\,}_{\overset{\Delta }{\mathop{ABC}}\,}}$

مساحت ناحیه هاشور خورده$=S{{\,}_{\overset{\Delta }{\mathop{ABC}}\,}}-2(\frac{1}{4}S{{\,}_{\overset{\Delta }{\mathop{ABC}}\,}})=S{{\,}_{\overset{\Delta }{\mathop{ABC}}\,}}-\frac{1}{2}S{{\,}_{\overset{\Delta }{\mathop{ABC}}\,}}$

مساحت ناحیه هاشور خورده$=\frac{1}{2}S{{\,}_{\overset{\Delta }{\mathop{ABC}}\,}}$