** فصل 2: تبدیل‌های هندسی و کاربردها
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
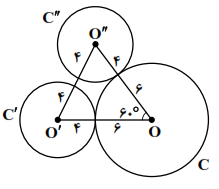
دایره‌ی $C(O,6)$ و ${C}'({O}',4)$ مماس خارج‌اند. در دورانی به مرکز O و زاویه‌ی ${{60}^{{}^\circ }}$، دایره‌ی ${C}'$ به دایره‌ی ${C}''({O}'',{R}'')$ تبدیل می‌شود. طول مماس مشترک داخلی دو دایره‌ی ${C}'$ و ${C}''$ کدام است؟
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...