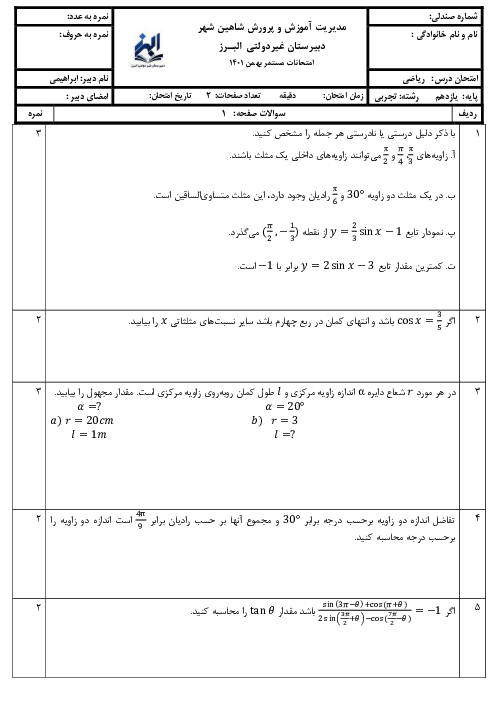
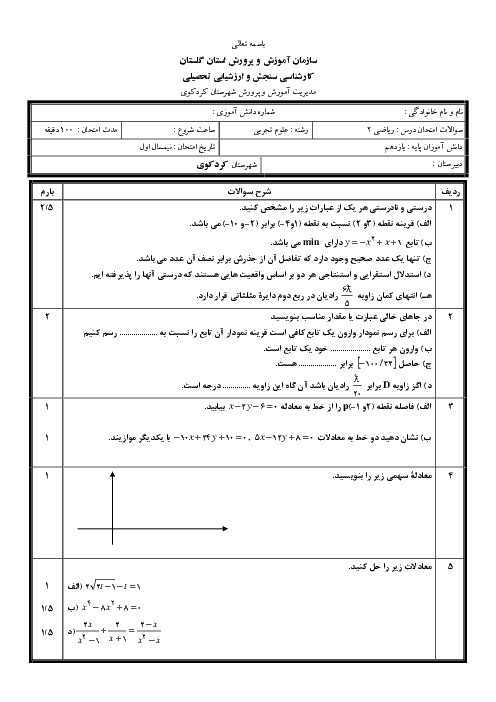
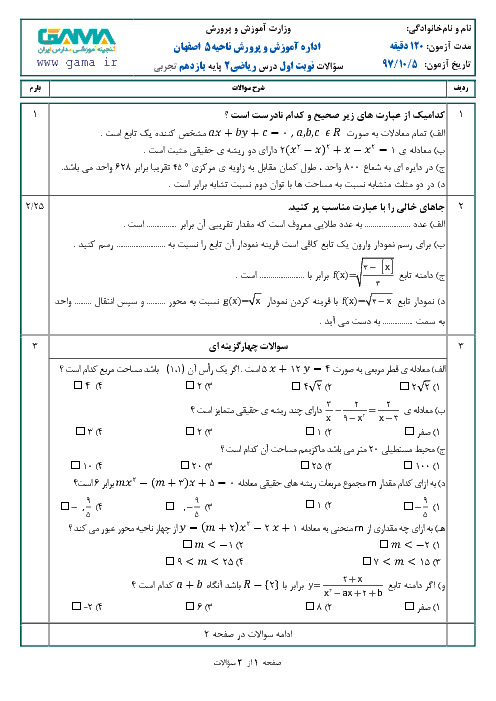
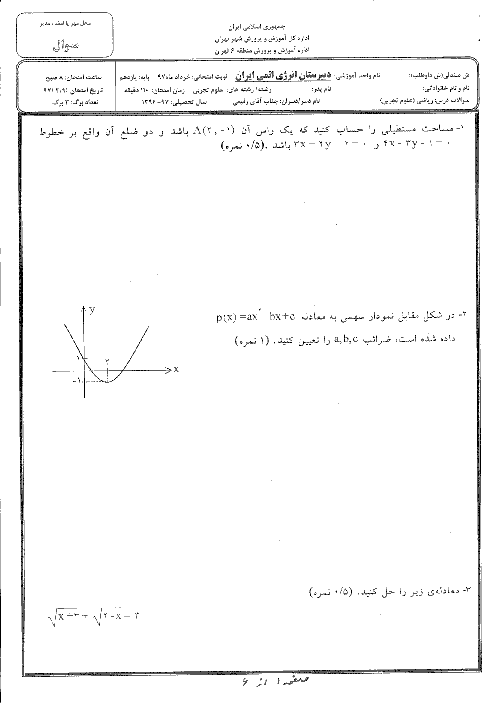
اگر طول ضلع های زاویه های قائمه ی مثلث را aوbوطول وتر آن را c فرض کنیم آن گاه :

$
\hspace{0.33em}\hspace{0.33em}\frac{a}{b}\mathrm{{=}}\frac{3}{4}\mathrm{\Rightarrow}{b}\mathrm{{=}}\frac{4}{3}{a}
$

بنابراین طول وتر برابر است با:

$
\hspace{0.33em}{c}\mathrm{{=}}\sqrt{{a}^{2}\mathrm{{+}}{b}^{2}}\mathrm{{=}}\sqrt{{a}^{2}\mathrm{{+}}\frac{\mathrm{16}}{9}{a}^{2}}
$$
\hspace{0.33em}\mathrm{{=}}\sqrt{\frac{\mathrm{25}{a}^{2}}{9}}\hspace{0.33em}\hspace{0.33em}
$

بنابراین:

$
\frac{1}{a}\mathrm{{+}}\frac{1}{b}\mathrm{{+}}\frac{1}{c}\mathrm{{=}}\frac{\mathrm{47}}{\mathrm{30}}
$$
\hspace{0.33em}\mathrm{\Rightarrow}\frac{1}{a}\mathrm{{+}}\frac{1}{\frac{4}{3}a}\mathrm{{+}}\frac{1}{\frac{5}{3}a}\mathrm{{=}}\frac{\mathrm{47}}{\mathrm{30}}\mathrm{\Rightarrow}
$
$
\hspace{0.33em}\frac{1}{a}\mathrm{{+}}\frac{3}{4a}\mathrm{{+}}\frac{3}{5a}\mathrm{{=}}\frac{\mathrm{47}}{\mathrm{30}}
$

دوطرف معادله را در 60a ضرب می کنیم:

$
{\mathrm{60}}\mathrm{{+}}{\mathrm{45}}\mathrm{{+}}{\mathrm{36}}\mathrm{{=}}{\mathrm{94}}{a}\mathrm{\Rightarrow}
$$
{a}\mathrm{{=}}\frac{\mathrm{141}}{\mathrm{94}}\mathrm{{=}}\frac{3}{2}\mathrm{\Rightarrow}{b}\mathrm{{=}}{2}
$

بنابراین مساحت مثلث برابر است با :

S=$
\hspace{0.33em}\frac{1}{2}{ab}\mathrm{{=}}\frac{1}{2}\mathrm{\times}\frac{3}{2}\mathrm{\times}{2}\mathrm{{=}}\frac{3}{2}
$