درس 2: ضرب داخلی و ضرب خارجی بردارها
هندسه (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
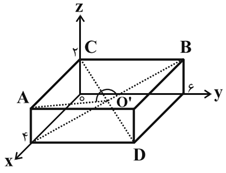
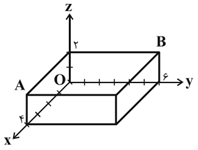
مطابق شكل زير، يک مكعب مستطيل روی محورهای مختصات تشكيل شده است. اگر ${O}'$ نقطهٔ برخورد قطرهای مكعب مستطيل باشد، مقدار $\cos (\widehat{A{O}'B})$ كدام است؟
1 )
$\frac{-5}{6}$
2 )
$-\frac{3}{4}$
$\frac{-6}{7}$
4 )
$\frac{-2}{3}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...