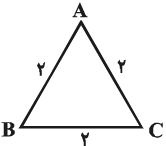
با توجه به مثلث متساوی‌الاضلاع $ABC$ داریم:

$\left\{ \begin{matrix}    \overrightarrow{AB}.\overrightarrow{BC}=\left| \overrightarrow{AB} \right|\left| \overrightarrow{BC} \right|\cos {{120}^{\circ }}=2\times 2\times \left( -\frac{1}{2} \right)=-2  \\    \overrightarrow{AC}.\overrightarrow{CB}=\left| \overrightarrow{AC} \right|\left| \overrightarrow{CB} \right|\cos {{120}^{\circ }}=2\times 2\times \left( -\frac{1}{2} \right)=-2  \\ \end{matrix} \right.$ 

$\Rightarrow (\overrightarrow{AC}.\overrightarrow{CB})\overrightarrow{AB}-(\overrightarrow{AB}.\overrightarrow{BC})\overrightarrow{AC}=-2\overrightarrow{AC}=2(\overrightarrow{AC}-\overrightarrow{AB})=2\overrightarrow{BC}$ 

تذكر: دقت كنيد كه زاويه‌ی بين بردارهای $\overrightarrow{AB}$ و $\overrightarrow{BC}$ و نیز $\overrightarrow{AC}$ و $\overrightarrow{CB}$، مکمل زاویه‌های $B$ و $C$ در مثلث متساوی‌الاضلاع $ABC$ است، چون ابتدا يا انتهای هر جفت از اين بردارها بر نقطه‌ی $B$ یا $C$ منطبق نیست.