قسمت 3: حرکت با شتاب ثابت
فیزیک (3) تجربی
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
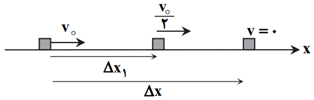
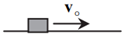
مطابق شكل، جسم كوچكی توسط ضربه‌ای با سرعت اوليۀ ${{v}_{{}^\circ }}$ روی سطح افقی به حركت درمی‌آيد. حركت ذره با شتاب ثابت و كندشونده است. جابه‌جايی جسم از لحظۀ شروع حركت تا لحظه‌ای كه سرعت $\frac{{{v}_{{}^\circ }}}{2}$ است، چند برابر جابه‌جايی ازلحظۀ شروع حرکت تا توقف کامل است؟
1 )
$\frac{1}{2}$
2 )
$\frac{1}{4}$
$\frac{3}{4}$
4 )
$\frac{\sqrt{2}}{2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...