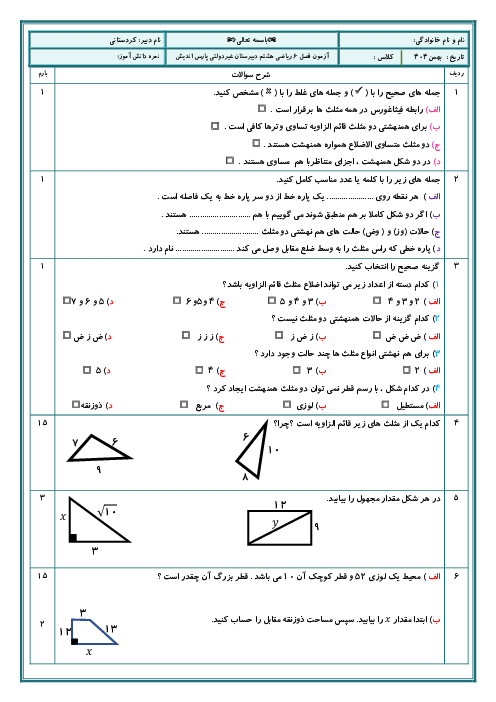
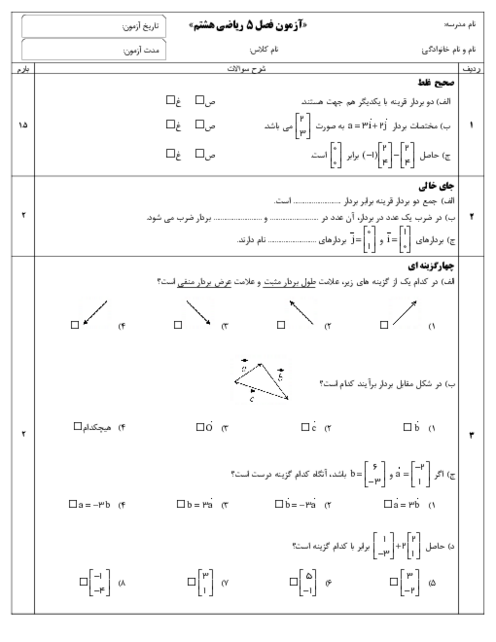
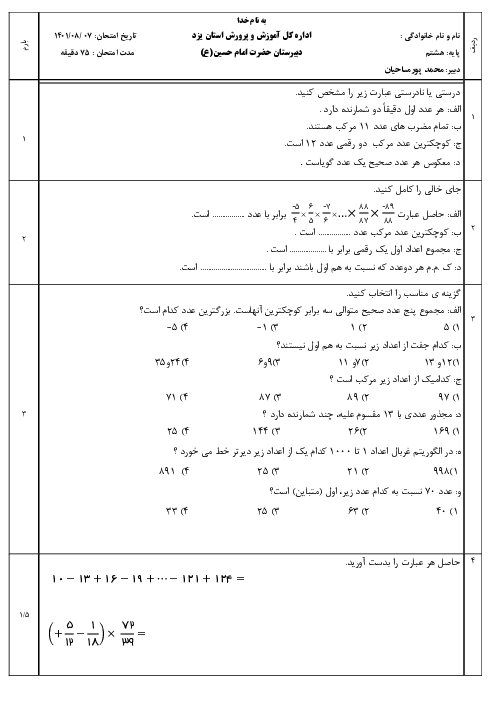
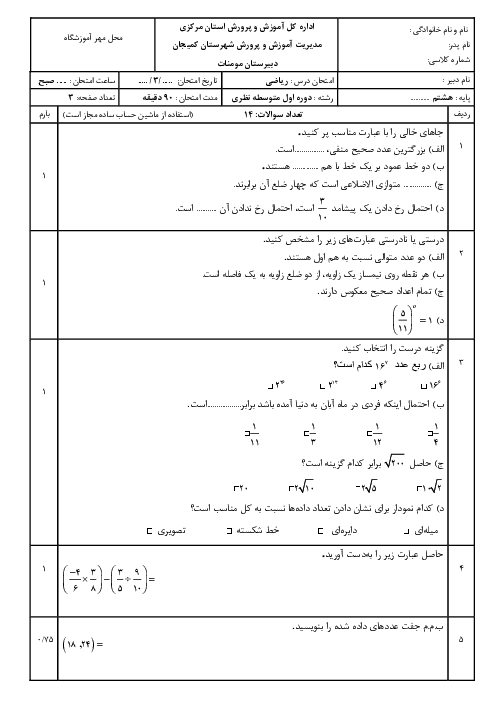
بردار‌ها را به دو طریق می‌توان نوشت:

الف) به صورت مختصات طول و عرض بنویسیم یعنی: $\left[ \begin{matrix}    a  \\    b  \\ \end{matrix} \right]$ که $a$ طول و $b$ عرض است.

ب) یا به صورت واحد‌های مختصات $\overrightarrow{j},\overrightarrow{i}$ نمایش داده می‌شود. یعنی: $\left[ \begin{matrix}    a  \\    b  \\ \end{matrix} \right]=a\overrightarrow{i}+b\overrightarrow{j}$ که $\overrightarrow{i}$ واحد طول یعنی $\overrightarrow{i},\left( \overrightarrow{i}=\left[ \begin{matrix}    1  \\    0  \\ \end{matrix} \right] \right)$ واحد عرض یعنی: $\left( \overrightarrow{i}=\left[ \begin{matrix}    0  \\    1  \\ \end{matrix} \right] \right)$

* توجه: در جمع و تفریق بردار‌ها طول‌ها را با هم جمع می‌کنیم و عرض‌ها را نیز با هم جمع می‌کنیم (توجه داشته باشیم که جمع جبری می‌شود. جبری؟) مانند: 

$\left[ \begin{matrix}    a  \\    b  \\ \end{matrix} \right]+\left[ \begin{matrix}    c  \\    d  \\ \end{matrix} \right]=\left[ \begin{matrix}    a+c  \\    b+d  \\ \end{matrix} \right]$

* در ضرب یک عدد در بردار: آن عدد هم باید در طول بردار و هم در عرض بردار ضرب شود. مانند:

$k\left[ \begin{matrix}    a  \\    b  \\ \end{matrix} \right]=\left[ \begin{matrix}    ka  \\    kb  \\ \end{matrix} \right]$

پس: 

$\overrightarrow{a}=-4\overrightarrow{i}+2\overrightarrow{j}=-4\left[ \begin{matrix}    1  \\    0  \\ \end{matrix} \right]+2\left[ \begin{matrix}    0  \\    1  \\ \end{matrix} \right]=\left[ \begin{matrix}    -4  \\    0  \\ \end{matrix} \right]+\left[ \begin{matrix}    0  \\    2  \\ \end{matrix} \right]=\left[ \begin{matrix}    -4  \\    2  \\ \end{matrix} \right]$ 

 $\overrightarrow{b}=\frac{1}{2}\overrightarrow{a}=\frac{1}{2}\left[ \begin{matrix}    -4  \\    2  \\ \end{matrix} \right]=\left[ \begin{matrix}    \frac{1}{2}\times \left( -4 \right)  \\    \frac{1}{2}\times 2  \\ \end{matrix} \right]=\left[ \begin{matrix}    -2  \\    1  \\ \end{matrix} \right]$ 

$\left. \begin{matrix}    \overrightarrow{a}=\left[ \begin{matrix}    -4  \\    2  \\ \end{matrix} \right]  \\    \overrightarrow{b}=\left[ \begin{matrix}    -2  \\    1  \\ \end{matrix} \right]  \\ \end{matrix} \right\}\Rightarrow \overrightarrow{x}=\overrightarrow{a}-3\overrightarrow{b}=\left[ \begin{matrix}    -4  \\    2  \\ \end{matrix} \right]-3\left[ \begin{matrix}    -2  \\    1  \\ \end{matrix} \right]=\left[ \begin{matrix}    -4  \\    2  \\ \end{matrix} \right]+\left[ \begin{matrix}    6  \\    -3  \\ \end{matrix} \right]=\left[ \begin{matrix}    2  \\    -1  \\ \end{matrix} \right]$