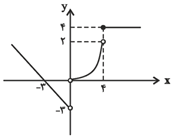
برد تابع چند ضابطهای زير كدام است؟
$f(x)=\left\{ \begin{matrix} -x-3;x\lt 0 \\ \frac{1}{8}{{x}^{2}};0\lt x\lt 4 \\ 4;x\ge 4 \\ \end{matrix} \right.$
1 )
$(-\infty ,-3)\bigcup (0,4)$
$(-3,+\infty)$
3 )
$\left( -\infty ,4 \right]$
4 )
$(-\infty ,2)\bigcup \left\{ 4 \right\}$
پاسخ تشریحی :
تحلیل ویدئویی تست
زهرا شیخ الاسلامی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...