درس 1: تفکر تجسمی و آشنایی با مقاطع مخروطی
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
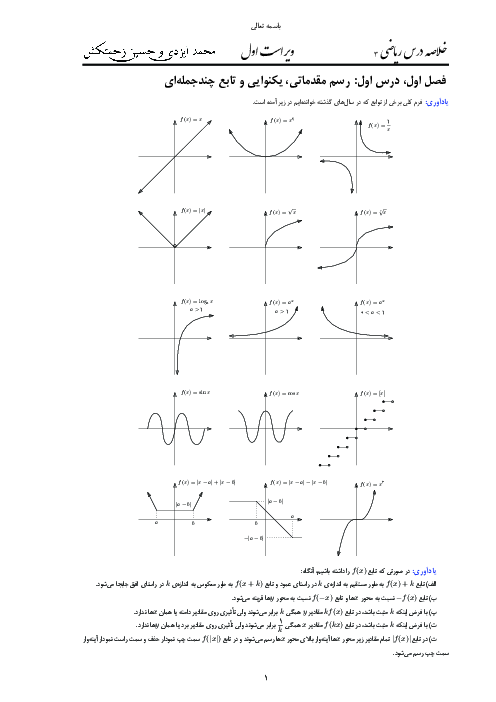
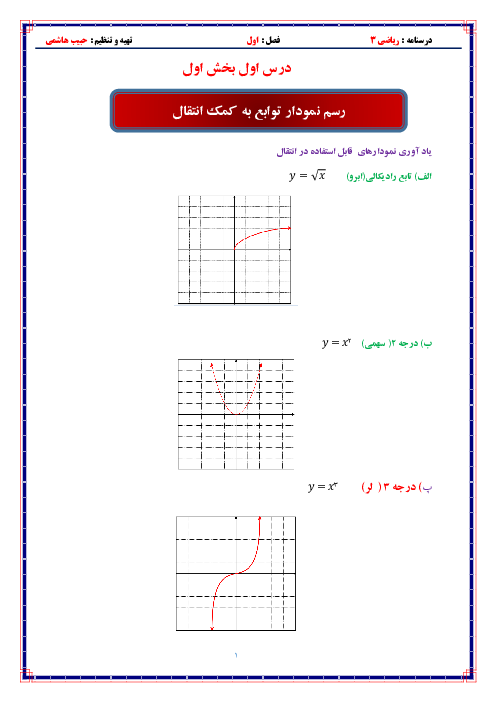
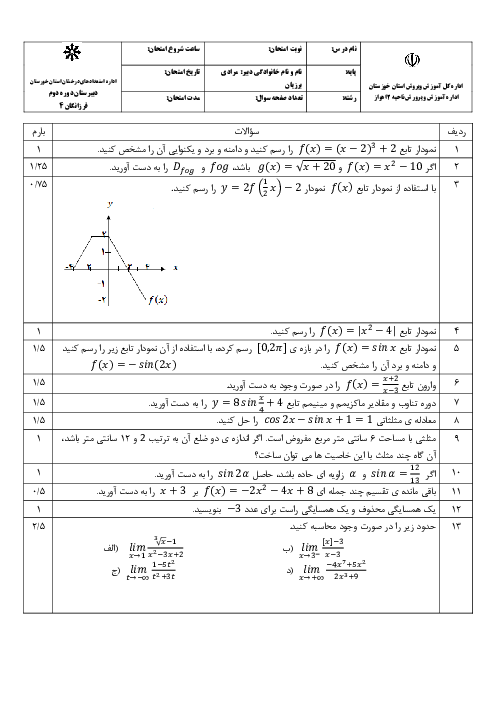
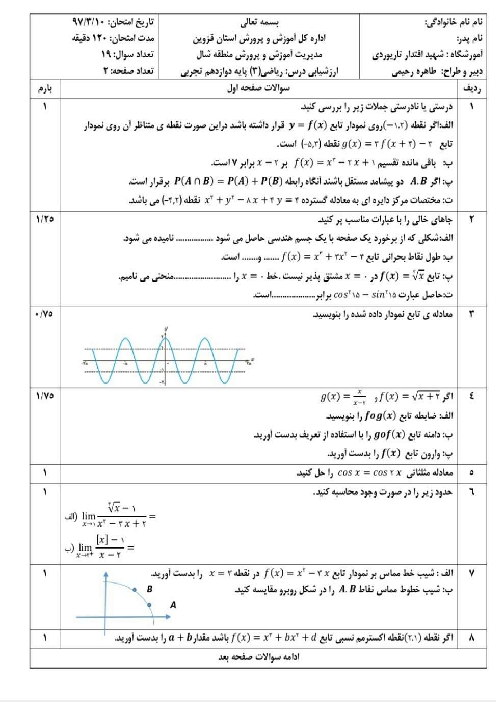
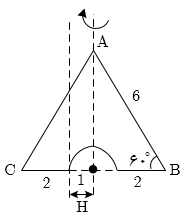
یک نیم‌دایره را مطابق شکل از یک مثلث متساوی‌الاضلاع بریده و شکل حاصل را حول محور تقارنش دوران می‌دهیم. حجم شکل حاصل از این دوران کدام است؟
$(9\sqrt{3}-\frac{4}{3})\pi $
2 )
$(6\sqrt{3}-\frac{2}{3})\pi $
3 )
$(9\sqrt{3}-\frac{2}{3})\pi $
4 )
$(6\sqrt{3}-\frac{4}{3})\pi $
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...