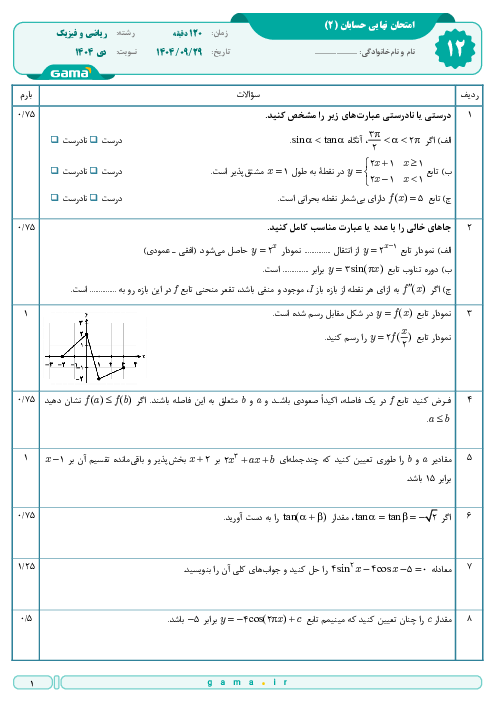
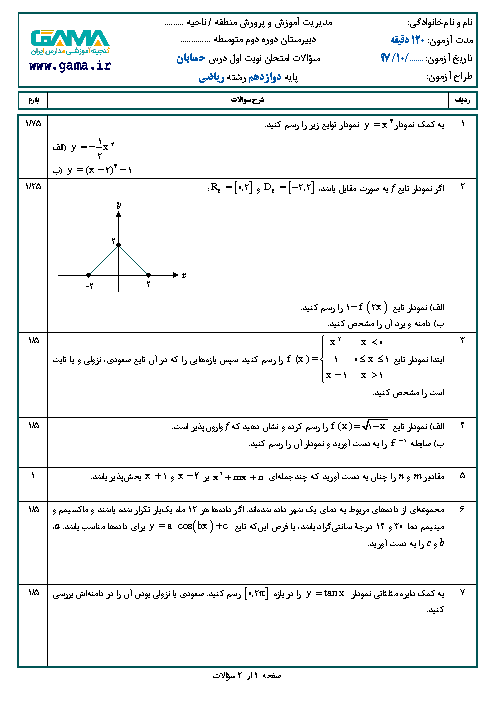
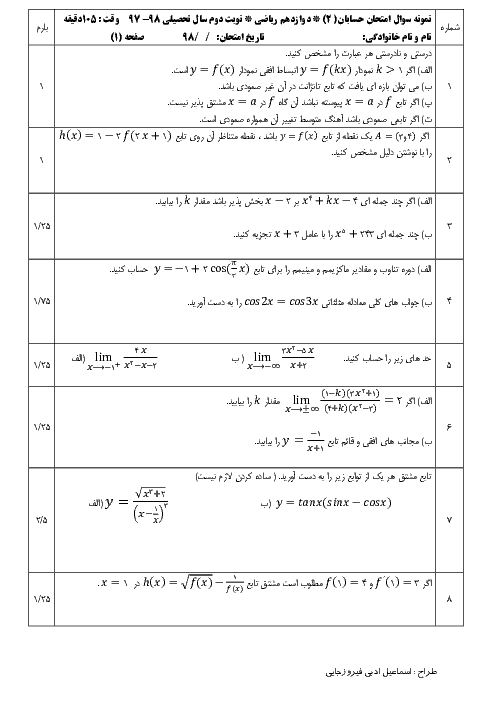
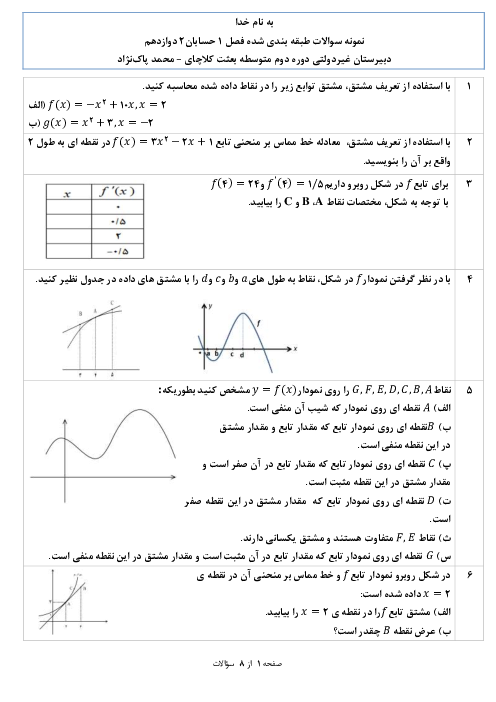
درس 1: اکسترممهای یک تابع و توابع صعودی و نزولی
حسابان (2)
دوازدهم
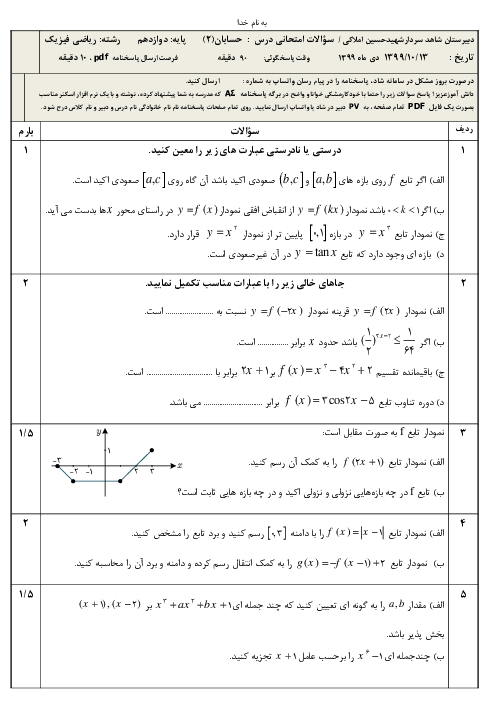
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
حاصل ضرب مقادير ماكزيمم و مينيمم مطلق تابع $f\left( x \right)={{x}^{2}}-6x+a$ در بازهٔ $\left[ 1,4 \right]$ برابر $P$ است. حداقل مقدار $P$ كدام است؟