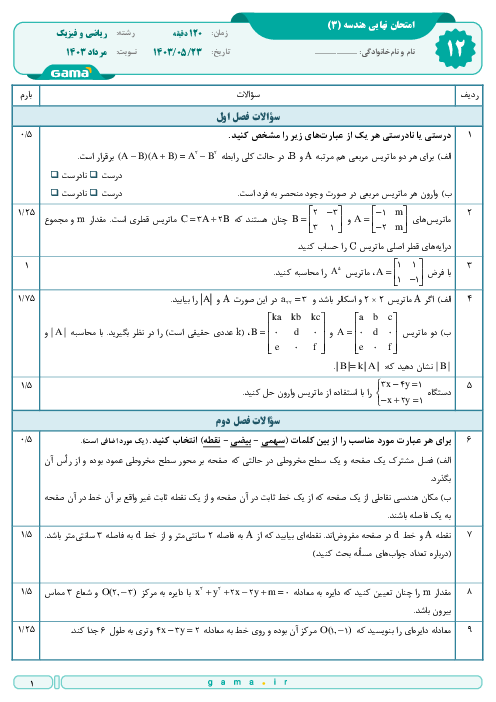
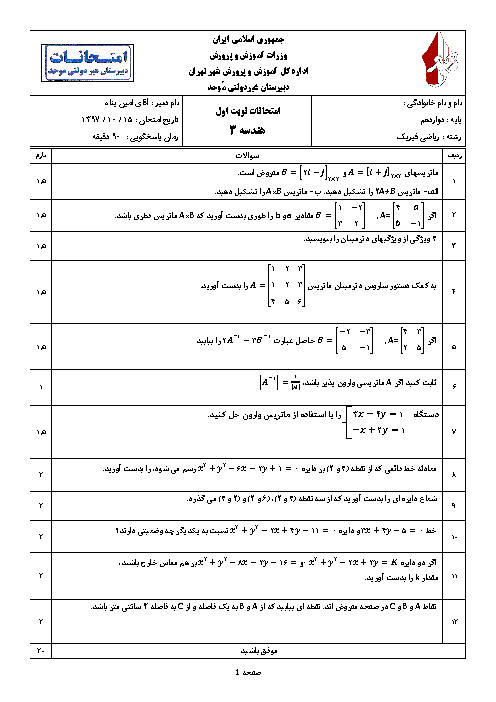
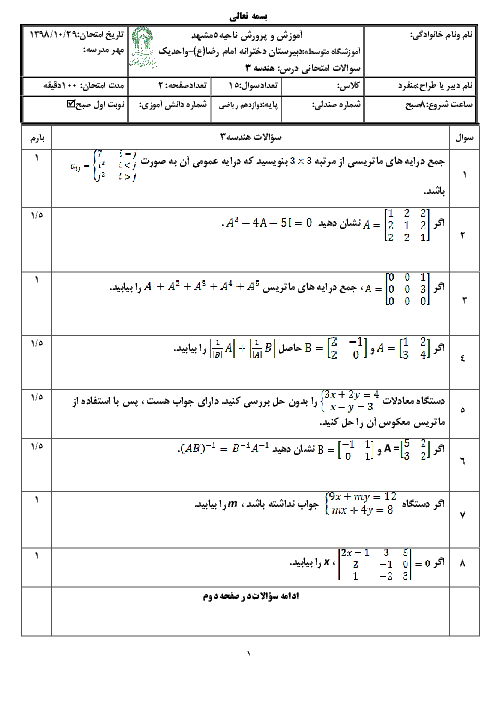
اگر $A=\left[ \begin{matrix}
0 & \tan x \\
\cot x & 0 \\
\end{matrix} \right]$ باشد، حاصل $\left[ \begin{matrix}
2 & 1 \\
-1 & 5 \\
\end{matrix} \right]{{A}^{10}}\left[ \begin{matrix}
1 & 2 \\
3 & 4 \\
\end{matrix} \right]$ کدام است؟
1 )
$\left[ \begin{matrix}
{{\tan }^{9}}x & 3 \\
3 & {{\cot }^{9}}x \\
\end{matrix} \right]$
$\left[ \begin{matrix}
5 & 8 \\
14 & 18 \\
\end{matrix} \right]$
3 )
$\left[ \begin{matrix}
{{\tan }^{10}}x & 2 \\
2 & {{\cot }^{10}}x \\
\end{matrix} \right]$
4 )
$\left[ \begin{matrix}
14 & 18 \\
5 & 8 \\
\end{matrix} \right]$