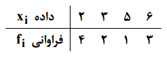نكته: داده‌ای كه بيش‌ترين فراوانی را داشته باشد، مد يا نما نام دارد. 

نكته: اگر $n$ دادهٔ ${{x}_{1}}$، ${{x}_{2}}$، ...، ${{x}_{n}}$، داشته باشيم به‌طوری كه هريک از اين داده‌ها دارای تعداد تكرار ${{w}_{1}}$، ${{w}_{2}}$، ...، ${{w}_{n}}$ باشند (که به هریک از آن‌ها وزن دادهٔ متناظر به آن می‌گوييم)، ميانگين موزون داده‌ها را با نماد ${{\overline{x}}_{w}}$ نشان می‌دهیم و آن را به‌صورت زیر تعریف می‌کنیم:

${{\overline{x}}_{w}}=\frac{\sum\limits_{i=1}^{n}{{{w}_{i}}{{x}_{i}}}}{\sum\limits_{i=1}^{n}{{{w}_{i}}}}=\frac{{{w}_{1}}{{x}_{1}}+{{w}_{2}}{{x}_{2}}+...+{{w}_{n}}{{x}_{n}}}{{{w}_{1}}+{{w}_{2}}+...+{{w}_{n}}}$

با توجه به تعريف مد، در جدول مقابل عدد 2 دارای بيش‌ترين فراوانی بوده و مد می‌باشد، ميانگين نيز برابر است با: 

$\frac{{{x}_{i}}}{{{w}_{i}}},\frac{2}{4},\frac{3}{2},\frac{5}{1},\frac{6}{3}$                        $\overline{x}=\frac{2\times 4+3\times 2+5\times 1+6\times 3}{10}=\frac{37}{10}=3/7$

بنابراين اختلاف مد و ميانگين برابر $3/7-2=1/7$ است.