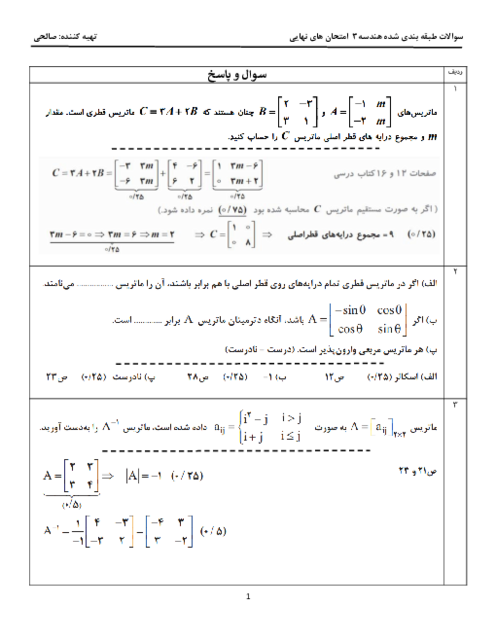
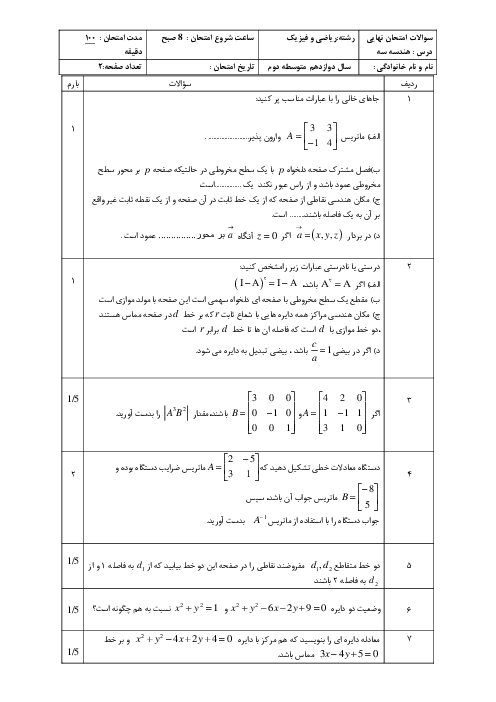
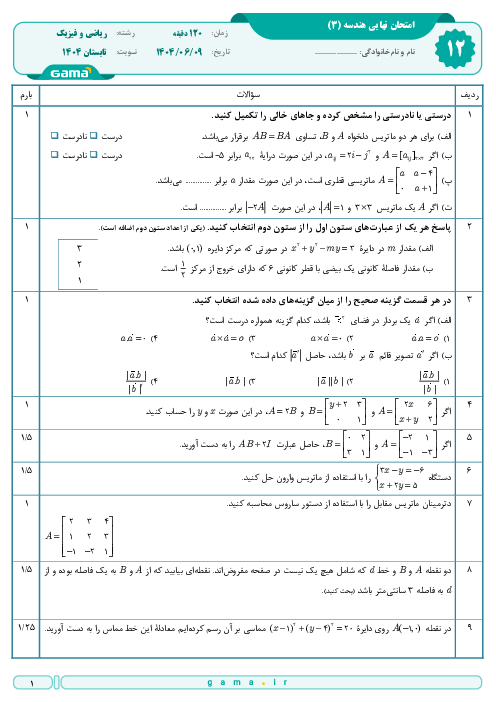
نکته: اگر $A=\left[ \begin{matrix}    a & b  \\    c & d  \\ \end{matrix} \right]$ ، آن‌گاه وارون $A$ یعنی ${{A}^{-1}}$ از رابطۀ زير به‌دست می‌آيد:

${{A}^{-1}}=\frac{1}{\left| A \right|}\times \left[ \begin{matrix}    d & -b  \\    -c & a  \\ \end{matrix} \right];\left| A \right|=ad-bc$ 

با توجه به نكته بالا داريم:

$A+I=\left[ \begin{matrix}    -2 & 3  \\    -1 & 1  \\ \end{matrix} \right]+\left[ \begin{matrix}    1 & 0  \\    0 & 1  \\ \end{matrix} \right]=\left[ \begin{matrix}    -1 & 3  \\    -1 & 2  \\ \end{matrix} \right]\Rightarrow \left| A+I \right|=-2+3=1$ 

$\Rightarrow {{\left( A+I \right)}^{-1}}=\frac{1}{1}\times \left[ \begin{matrix}    2 & -3  \\    1 & -1  \\ \end{matrix} \right]=\left[ \begin{matrix}    2 & -3  \\    1 & -1  \\ \end{matrix} \right]\Rightarrow 2{{\left( A+I \right)}^{-1}}=\left[ \begin{matrix}    4 & -6  \\    2 & -2  \\ \end{matrix} \right]$