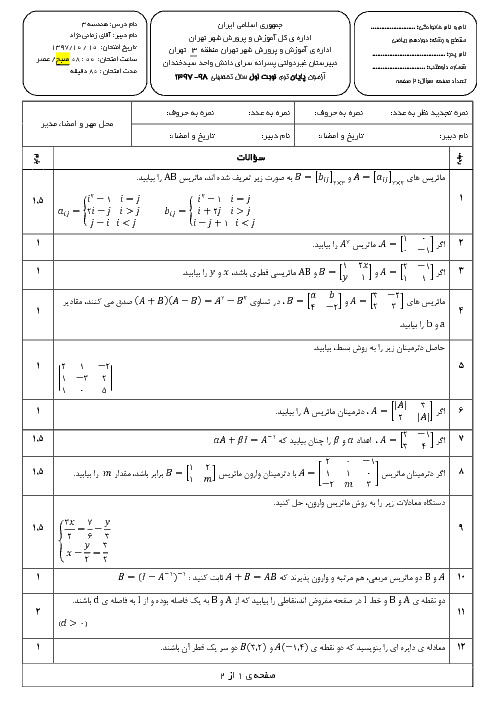
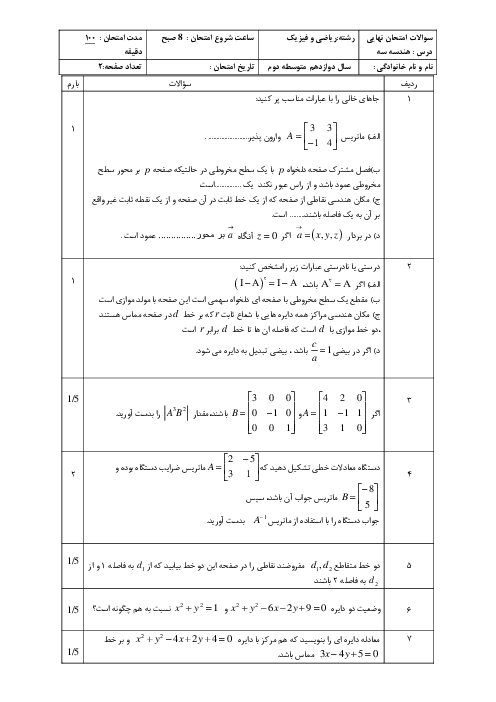
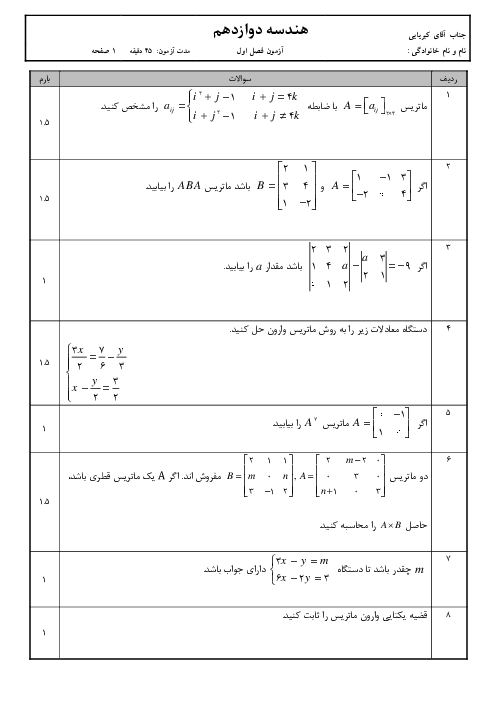
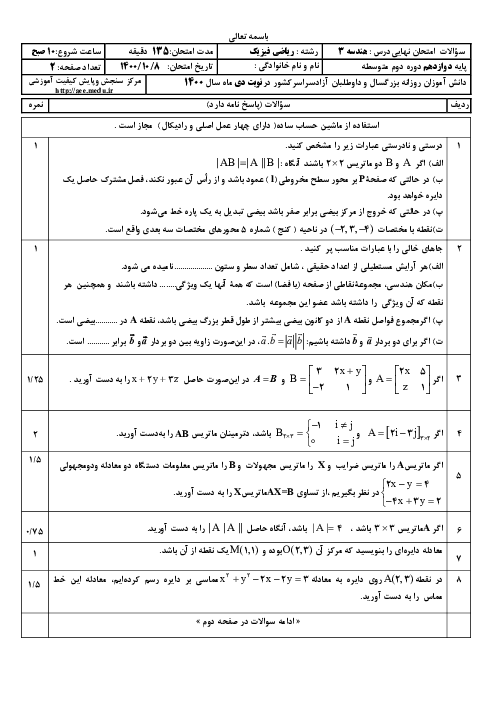
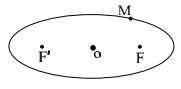
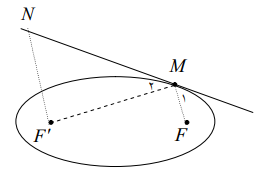
در شکل مقابل نقطه M روی بیضی و کانون‌های $F$ و $F'$ مشخص شده‌اند. خط d را به گونه‌ای رسم کنید که در نقطه M بر بیضی مماس باشد و سپس از نقطه $F'$ خطی موازی با MF رسم کنید تا خط d را در نقطه‌ای مانند N قطع کند. ثابت کنید: $NF' = MF'$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...