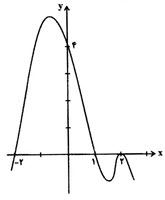
$f\left( x \right)=k\left( x+2 \right)\left( x-1 \right){{\left( x-2 \right)}^{2}}$ 

$\left( 0,4 \right)\in f\Rightarrow f\left( 0 \right)=4=-8k\Rightarrow k=-\frac{1}{2}\Rightarrow f\left( x \right)=-\frac{1}{2}\left( x+2 \right)\left( x-1 \right){{\left( x-2 \right)}^{2}}$ 

باقی‌مانده‌ی تقسیم $f\left( x \right)$ بر ${{x}^{2}}-2x-3$ را به صورت $ax+b$ در نظر می‌گیریم. 

${{x}^{2}}-2x-3=0\Rightarrow \left( x+1 \right)\left( x-3 \right)=0$ 

$\Rightarrow \left\{ \begin{matrix}    x=-1\Rightarrow f\left( -1 \right)=9  \\    x=3\Rightarrow f\left( 3 \right)=-5  \\ \end{matrix}\Rightarrow \left\{ \begin{matrix}    -a+b=9  \\    3a+b=-5  \\ \end{matrix} \right.\Rightarrow \left\{ \begin{matrix}    a-b=-9  \\    3a+b=-5  \\ \end{matrix} \right. \right.$ 

$\Rightarrow 4a=-14$ 

$\Rightarrow a=\frac{-14}{4},b=\frac{22}{4}\Rightarrow R\left( x \right)=-\frac{14}{4}x+\frac{22}{4}$