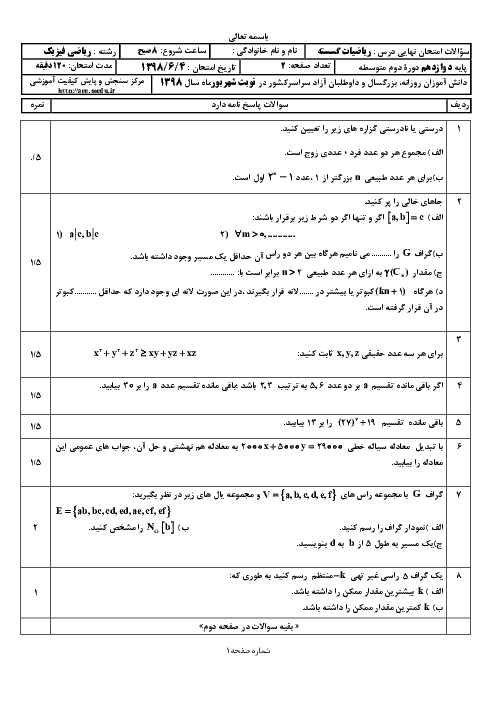
گزاره زیر را به روش بازگشتی (گزارههای همارز) ثابت کنید.
به ازای هر دو عدد حقیقی و دلخواه x و y داریم: $xy \leqslant \frac{{{x^2} + {y^2}}}{2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...