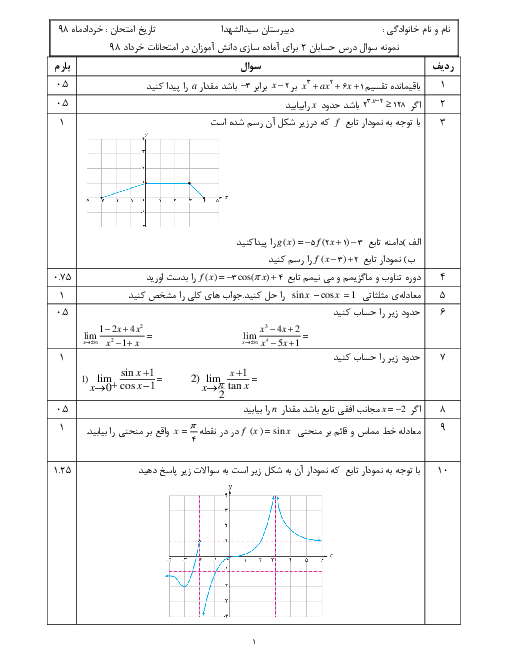
اگر $f$ تابعی اکیدا صعودی و گذرنده از مبدا و $\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f(x)=+\infty $ باشد، آنگاه:
$\underset{x\to +\infty }{\mathop{\lim }}\,{{f}^{-1}}(x)=1$
2 )
$\underset{x\to -\infty }{\mathop{\lim }}\,{{f}^{-1}}(x)=1$
3 )
$\underset{x\to +\infty }{\mathop{\lim }}\,{{f}^{-1}}(x)=۰$
4 )
$\underset{x\to -\infty }{\mathop{\lim }}\,{{f}^{-1}}(x)=۰$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...